Question 42827This question is from textbook Algebra Structure and Method Book 1
: Jessica has 16 dimes and quarters. Whitney has twice as many dimes and 1/3 as many quarters as Jessica has. If they both have the same amount of money, what coins do each have?
This question is from textbook Algebra Structure and Method Book 1
Answer by aaaaaaaa(138)   (Show Source):
You can put this solution on YOUR website! Let's denote the number of dimes Jessica has by d and the number of quarters she has by q.
The first sentence tells us that:
Whitney has twice as many dimes (2d) and 1/3 as many quarters (1/3q) and they have the same amount of money. We could try to say  , but that's not true, as d and q have different value. Our equation, with the weight of the values in, is:
We can simplify it by multiplying the 2, getting:
Then, we can subtract 20d and 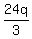 from both sides of the equation and solve the system:
| Solved by pluggable solver: SOLVE linear system by SUBSTITUTION |
Solve:
 We'll use substitution. After moving 1*q to the right, we get:
 , or  . Substitute that
into another equation:
 and simplify: So, we know that q=5.99999999999999. Since , d=10.
Answer:  .
|
Therefore, Jessica has 10 dimes and 6 quarters, and Whitney has 2*10 = 20 dimes and 1/3 * 6 = 2 quarters.
We can check by seeing that 10*10 + 25*6 = 250, and 20*10 + 25*2 is also 250.
|
|
|
