Question 42824: Hi! I'm trying to figure out a problem with a hexagon. I need to find the side of a regular hexagon if the it is 18 inches apart from midpoint to midpoint. Any help would be greatly appreciated!
Thankyou!
Found 2 solutions by fractalier, psbhowmick:
Answer by fractalier(6550)   (Show Source): (Show Source):
You can put this solution on YOUR website! You can use trig to do this...
Make a triangle with the segment connecting the midpoints of the sides as the base...
Then bisect the top angle and drop an altitude, making two right triangles...
Each right triangle has a top angle of 67.5 degrees...the long leg is 9, which is half of the 18...the hypotenuse is half the side of the hexagon...
Thus sin 67.5 = 9/x and
x = 9 / (sin 67.5) = 9.74
and the side is double that, or about
19.48 inches
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your statement of the problem is not very clear.
I assume, what you meant is: The side of a regular hexagon in which the distance between the opposite sides is 18".
See the regular hexagon ABCDEF below.

According to the problem the distance between sides AB & DE, BC & EF and CD & FA is 18" and we are required to find length AB or any other side.
Join B and F with a straight line. Then drop a perpendicular to BF from A intersecting BF at G.

Now, in triangle ABF,
BF = 18",
< BAF =  [since each internal angle of a regular hexagon is [since each internal angle of a regular hexagon is  ] ]
Clearly, triangle ABG and triangle AFG are congruent.
So, < BAG =  < BAF = < BAF =  and BG = and BG =  BF = 9". BF = 9".
Now, in triangle ABG,
< AGB =  [since AG is perpendicular to BF] [since AG is perpendicular to BF]
So in right angled triangle AGB,
sin(< BAG) = 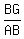
or sin = = 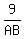
or AB = 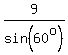 " = " = 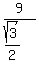 " = " =  " = 10.4" (approx) " = 10.4" (approx)
Thus the reqd. side of the regular hexagon is approximately 10.4 inches.
|
|
|