Question 42819: Hi,
You guys are great! Yoy helped with a problem we had before and broke it down so we understood! So here we go again! Thanks for all your help!
1) Your company sells 2 products: A and B. A sells for $12.00 and B sells for $10.00. The cost to make the products is $9.00 for A and $8.00 for B. Our objective is to maximize profit.
(A) can be made in quantites between 200 and 300 units
(B) can be made in quantites between 100 and 250 units
Total units produced for A and B cannot exceed 500
Questions:
1) Identify the objective function
2) Graph the region bounded by the constraints
3) Identify the vertices found in #2
4) For each vertex, compute the value of the objective function
5) Determine the quantites of each product that should be made to maximize profit.
---------------------------------------------------------------------------
Okay here are my thoughts but I am completely confused!
1) f(x)=?
2) 200 <=A=> 300 and 100 <=b=> 250 is range and a+b>=500
3) ?
4) ?
5) ?
______________________________________________________________________________
#2
We have 3 products: A, B and C. Each could be made in one of 3 factories: X, Y, and Z. Each product requires design, assembly, and finishing. Given the information in the tables below, determine which factory should make each product. Assume labor costs are the only considerations.
Table:1 Table 2: Hourly Wage rates
Design Assembly Finishing X Y Z
A 10 5 2 Design 6 8 8
B 6 4 3 Assembly 5 3 3
C 12 6 2 Finishing 4 3 2
_____________________________________________________________________________
This problem --I am completely lost! Please help!
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a LP (Linear Programming) problem. It is not an algebra problem at all. I have done such problems in our Industrial Management class last semester (also my final semester in Bachelor of Engineering). Though it is not algebra, I am solving this one. Here you go....
Let the no. of products A sold be 'x' and that of product B sold be 'y'.
Then cost of production of all the products = $(9x + 8y).
Selling price of all the products = $(12x + 10y).
Hence, overall profit = $(12x + 10y) - $(9x + 8y) = $(3x + 2y).
So the objective function is: f(x,y) = 3x + 2y.
The constraints are:
 , ,  and and 

Pentagon ABCDE is the required region bounded by constraints.
The vertices are A(200,250), B(250,250), C(300,200), D(300,100) and E(200,100).
For the vertex A(200,250), the value of objective function is f(x,y) = f(200,250) = 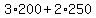 = 1100. = 1100.
Similarly, the other objective functions at B, C, D and E are 1250, 1300, 1100 and 800 respectively.
Profit will be maximum when the number of units produced will be maximum.
Maximum number of units that can be procuded is 500 so the values of x & y for maximum profit will lie on line BC.
Keeping total number of units produced same, at 500 (which is maximum value), the profit is maximized when the no. of units of A [in which profit per unit ($3) is more than in B (2$)] produced is of the maximum possible value. This condition is satisfied by the coordinates of the point C.
Hence, for maximum profit 300 units of A and 200 units of B have to be produced and sold.
I have shown you the process.
Do the next one yourself because more you do these problems yourself, better you learn.
|
|
|