SOLUTION: Quadrilateral MATH has coordinates M(1,1), A(-2,5), T(3,5), and H(6,1). Prove that quadrilateral MATH is a rhombus and prove that it is not a square. Thank you:)

Algebra ->  Geometry-proofs -> SOLUTION: Quadrilateral MATH has coordinates M(1,1), A(-2,5), T(3,5), and H(6,1). Prove that quadrilateral MATH is a rhombus and prove that it is not a square. Thank you:)      Log On


   

Question 428189: Quadrilateral MATH has coordinates M(1,1), A(-2,5), T(3,5), and H(6,1). Prove that quadrilateral MATH is a rhombus and prove that it is not a square.
Thank you:)
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!


Hi

D = 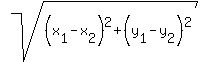sqrt+%28%28x%5B1%5D-x%5B2%5D%29%5E2%2B%28y%5B1%5D-y%5B2%5D%29%5E2%29%29

M(1,1), 

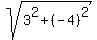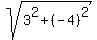A(-2,5), MA= sqrt%283%5E2%2B%28-4%29%5E2%29=5   m = -4/3  m+=%28y%5B2%5D+-+y%5B1%5D%29%2F%28x%5B2%5D+-+x%5B1%5D%29

T(3,5),  AT= sqrt%283%5E2%2B%28-4%29%5E2%29=5   m = 0

H(6,1).  TH= 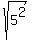sqrt%285%5E2%29=5          m = -4/3

M(1,1),  HM= 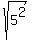sqrt%285%5E2%29=5          m= 0

All 4 sides have equal length,opposite sides parallel

adjacent sides are not perpendicular(slopes are NOT negative reciprocals) 

Rhombus but not a Square.