|
Question 428079: I need help with this word problem.
A decorative slate centerpiece for a kitchen island has the shape of a rectangle with a semicircular section attached at each end.The radii of the semicircles measure x/2 inches.The perimeter of the centerpiece is 38 inches.Write a completely factored polynomial whose values give the area of the centerpiece.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the radius of each of the semi-circles is equal to x/2.
since the semi-circles are attached at each end of the rectangle, then the width of the rectangle is equal to the diameter of each semi-circle which is equal to 2 * the radius of each semi-circle which is equal to x.
if you take the 2 semi-circles and put them together then you have a complete circle.
the perimeter of the centerpiece is equal to 38 inches.
this encompasses the 2 lengths of the rectangle and the circumference of the 2 semi-circles put together.
the perimeter is therefore equivalent to 2 times the length of the rectangle plus the perimeter of the full circle.
we know that x is the width of the rectangle.
we set y equal to the length of the rectangle.
the perimeter of the centerpiece is therefore equal to 2*y + 2*pi*r.
r is the radius of the circle.
since r = x/2, then this formula becomes:
perimeter of centerpiece = 2*y + 2*pi*(x/2)
since the perimeter of centerpiece is equal to 38, then we get:
38 = 2*y + 2*pi*(x/2)
this reduces to 38 = 2*y + pi*x
if we solve for y, we get:
2y = 38 - pi*x which becomes:
y = (38 - pi*x) / 2
we now have a value for y in terms of x.
we have:
width of rectangle is x.
length of rectangle is (38 - pi*x) / 2
the area of the centerpiece is going to be the area of the rectangle plus the area of the circle.
remember that, if you put 2 semi-circles together, you get 1 circle.
the area of the centerpiece is therefore equal to length * width + pi*r^2.
pi*r^2 is the area of the circle.
length is equal to (38-pi*x)/2
width is equal to x
r is equal to (x/2)
area of the centerpiece is therefore equal to (38-pi*x)/2 * x + pi*(x/2)^2
this becomes:
(38*x)/2 - (pi*x^2)/2 + (pi*x^2)/4
bringing everything up to a common denominator gets us:
(76*x)/4 - (2*pi*x^2)/4 + (pi*x^2)/4
now that we have a common denominator, we can add all these together to get:
((76*x) - (2*pi*x^2) + (pi*x^2)) / 4
we combine like terms to get:
area of the centerpiece is equal to ((76*x) - (pi*x^2))/4
that's our equation.
it looks like this:
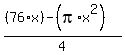
a picture of the centerpiece and it's equivalent structure is shown below:
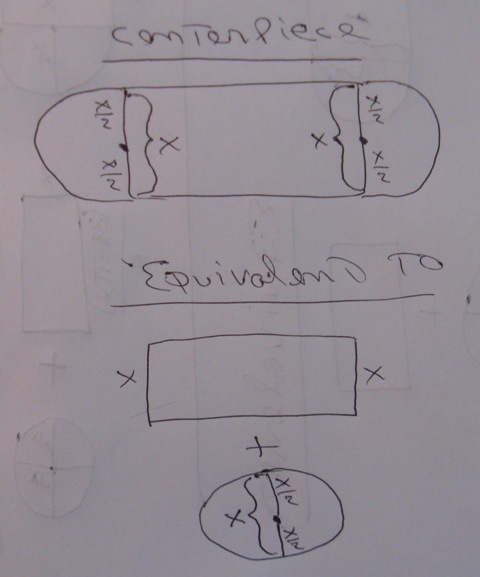
the perimeter is equal to the 2 lengths of the rectangle plus the cicumference of the circle.
the area is equal to the area of the rectangle plus the area of the circle.
in the picture, the lengths of the rectangle are the horizontal lines of the rectangle.
in the picture, the widths of the rectangle are the vertical lines of the rectangle.
the width of the rectangle is shown as x.
the length of the rectangle is not shown in the picture, but was previously shown as y which was then calculated to be (38-pi*x)/2.
|
|
|
| |