Question 42585: Cant remember how to solve this can anyone help
4000exp(-400t)-50000exp(-1000t)-64000exp(-1600t)=0
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Factor out the common factors, which would be 4000 and e raised to the lowest power of the variable, which is e^(-1600t). Remember that when you factor out the common factor, you must SUBTRACT exponents:
The common factor will be: 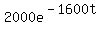


The first factor can never equal zero, so you need to solve:

Substitution may be helpful here, let  , then , then 
 , and this does NOT factor, so you'll have to use the quadratic formula to solve it. Then substitute the value back and solve for t. , and this does NOT factor, so you'll have to use the quadratic formula to solve it. Then substitute the value back and solve for t.
Solving with quadratic formula, you get
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=881 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 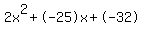 can be factored: can be factored:

Again, the answer is: 13.6704110398279, -1.17041103982791.
Here's your graph:
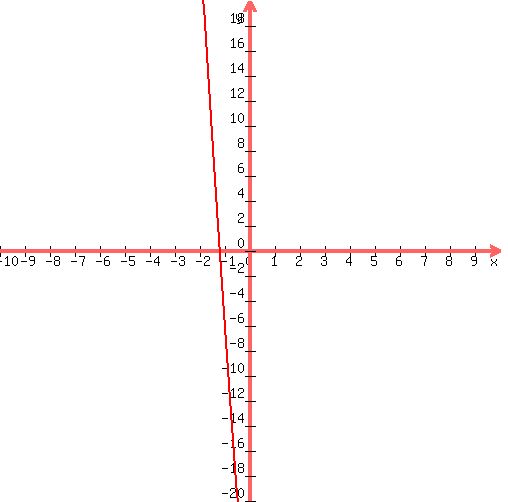 |
Now, 
so, to solve for t, will a decimal approximation be good enough? Otherwise it gets really hairy!!
 or or 
The second answer has no solution, since e raised to a power cannot equal a negative. This means that the first equation is the only one that has a solution.
You will need to take the ln of each side of this equation:

Divide both sides by 600:
 or approximately 0.00436 or approximately 0.00436
If you want to check this answer, you can always confirm the solution to this with a graphing calculator, using the "zeros" or the "root" method!!
By the way, the exact value of t would be  . Check it out, and see if the decimal approximation of this rounds off to 0.0043587229. . Check it out, and see if the decimal approximation of this rounds off to 0.0043587229.
R^2 at SCC
|
|
|