SOLUTION: 9^x=(1/27)^x+2 Please solve for x

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: 9^x=(1/27)^x+2 Please solve for x      Log On


   

Question 425715: 9^x=(1/27)^x+2
Please solve for x
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
I'm guessing your equation is:
9%5Ex=%281%2F27%29%5E%28x%2B2%29
If this is correct, then please put parentheses around multiple term exponents. For example: 9^x=(1/27)^(x+2)
If your equation is, as you posted,
9%5Ex=%281%2F27%29%5Ex%2B2
then you'll have to re-post it.

Solving equations like your, where the variable is in exponents is usually done in one of two ways:
  • If possible, rewrite the equation so that each side is a power of the same number. This is usually easier and faster than the next method but it is not always possible to rewrite an equation this way.
  • Use logarithms.

For the first method above, look to see if one base is a power of the other or if both bases are powers of some third number. Let's look at your equation>ul>
  • If you're really clever and understand exponents well, you know that 9 and 1/27 are powers of each other: 9%5E%28-3%2F2%29+=++1%2F27 and %281%2F27%29%5E%28-2%2F3%29+=+9.
  • If you're a little less clever you know that 9 and 27 (and their reciprocals) are both powers of 3:
    9+=+3%5E2
    27+=+3%5E3
    1%2F27+=+3%5E%28-3%29
  • And if you don't recognize either of the above, then there is always logarithms that can be used.

    • I'm going to show a solution based on each of the above three options. I'm going to start with the powers of 3 solution because I think is more likely you could see this solution than the first one.

    Replacing the 9 and the 1/27 in your equation with the powers of 3 that they are we get:
    %283%5E2%29%5Ex=%283%5E%28-3%29%29%5E%28x%2B2%29
    (Note the use of parentheses. When substituting one expression for another is is a good idea to use parentheses like this. It helps you see what should be done next.) On each side of the equation we have a power of a power of 3. The rule for exponents when raising a power to a pwower is to multiply the exponents:
    3%5E%282x%29=3%5E%28-3x-6%29
    We now have the equation with each side as a power of the same number. The only way two powers of 3 can be equal is if the exponents are equal, too. So:
    2x = -3x-6
    Now we solve for x. Adding 3x to each side we get:
    5x = -6
    Dividing by 5 we get:
    x+=+-6%2F5

    If we are clever enough to see that 9 is a power of 1/27 (and vice versa) then the solution is a little faster becauae we only have to replace one base. For example if we replace 1/27 with 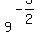9%5E%28-3%2F2%29 we get:
    9%5Ex+=+%289%5E%28-3%2F2%29%29%5E%28x%2B2%29
    which simplifies to
    9%5Ex+=+9%5E%28%28-3%2F2%29x-3%29
    Setting the exponents of 0 equal we get:
    x+=+%28-3%2F2%29x-3
    Solving for x. I woud start by eliminating the fraction by multiply by 2:
    2x+=+-3x-6
    which is the same equation as we had earlier. So it will have the same solution: x= -6/5

    For the logarithm solution we start by finding the logarithm of each side. Any base of logarithm can be used. However, choosing a base
    • that matches the base of one of the exponents will result in a simpler expression. With your equation this means choosing base 9 or base 1/27 logarithms.
    • that your calculator "knows", like base 10 or base e (aka ln), will lead to an expression that will be easier to turn into a decimal approximation if such an approximation becomes needed or wanted.
    I'm going to choose base 9 logarithms so I get a simpler expression:
    log%289%2C+%289%5Ex%29%29=log%289%2C+%28%281%2F27%29%5E%28x%2B2%29%29%29
    Next we use a property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, to move the exponents of the arguments out in front. (It is this very property of logarithms that is the very reason we use logarithms. The property let's us move the exponents, where the variable is, out in front where we can then solve for the variable.) Using this property on both logarithms:
    x%2Alog%289%2C+%289%29%29=%28x%2B2%29log%289%2C+%281%2F27%29%29
    log%289%2C+%289%29%29+=+1 by definition. (This is why matching the base of the logarithm to a base of one of the exponents results in s simpler expression.) So the left side becomes:
    x+=+%28x%2B2%29log%289%2C+%281%2F27%29%29
    Now we solve for x. Using the Distributive Property to simplify the right side we get:
    x+=+x%2Alog%289%2C+%281%2F27%29%29+%2B+2log%289%2C+%281%2F27%29%29
    Gathering the x terms on one side (by subtracting
    Factoring out x we get:
    x%2A%281+-+log%289%2C+%281%2F27%29%29%29+=+2log%289%2C+%281%2F27%29%29
    Dividing both sides by %281+-+log%289%2C+%281%2F27%29%29%29 we get:
    x+=+%282log%289%2C+%281%2F27%29%29%29%2F%281+-+log%289%2C+%281%2F27%29%29%29
    This may not look like the -6/5 that we found earlier. But it actually is. We just have to work a little more to simplify this. I'm going to use the change of base formula, log%28a%2C+%28p%29%29+=+log%28b%2C+%28p%29%29%2Flog%28b%2C+%28a%29%29 to convert the base 9 logarithms into base 3 logarithms. (I know this is what to do because 9 and 1/27 are powers of 3. So one way or another, we need to figure out this connection between 9, 1/27 and 3 in order to obtain a simplified, exact expression for the solution.)
    log%289%2C+%281%2F27%29%29+=+log%283%2C+%281%2F27%29%29%2Flog%283%2C+%281%2F27%29%29
    Since 9+=+3%5E2 and 1%2F27+=+3%5E%28-3%29, numerator is a -3 and the denominator is a 2:
    log%289%2C+%281%2F27%29%29+=+log%283%2C+%289%29%29%2Flog%283%2C+%281%2F27%29%29+=+-3%2F2
    Substituting -3/2 in for the logarithm in
    x+=+%282log%289%2C+%281%2F27%29%29%29%2F%281+-+log%289%2C+%281%2F27%29%29%29
    we get:
    x+=+%282%28-3%2F2%29%29%2F%281+-+%28-3%2F2%29%29
    which simplifies as follows:
    x+=+%28-3%29%2F%281+%2B+3%2F2%29
    x+=+%28-3%29%2F%282%2F2+%2B+3%2F2%29
    x+=+%28-3%29%2F%285%2F2%29
    x+=+%28-3%29%2A%282%2F5%29
    x+=+-6%2F5

    I hope after all this you are motivated to try to get both sides of the equation to be powers of the same number whenever possible. It is much easier than the logarithm method.