Question 42555: Find the sum of the infinite geometric series: 1 + 3/5 + 9/25 + ..., if it exists.
Thanks
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! The sum of the first 'n'-terms of a geometric series: a, ar, 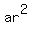 , ,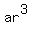 ,........., ,.........,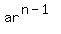 is given by is given by  when when 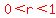 . .
When 'n' is very large, 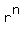 << 1 [means << 1 [means 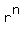 is very very less than 1]. is very very less than 1].
So, obviously when 'n' is infinity, 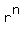 << 1 so it can be neglected (means taken as 0) in comparison to 1. << 1 so it can be neglected (means taken as 0) in comparison to 1.
Thus the summation formula for n =  becomes becomes

or 
Here, a = 1 and  so so 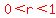 . .
Hence the formula of summation of geometric series for infinite number of terms (n ->  ) is applicable. ) is applicable.
Thus the summation of the given infinite geometric series is

or 
or 
Hence, the summation of the given series exists and its value is 2.5.
|
|
|