Question 424415: 1)For each gallon of gas you find you can go 26 miles, if you drive 20mph. You can go 34 miles if you go 40mph and 32 miles if you go 50mph. Find a quadratic function that models this data. What is the best speed to go with this model?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! For each gallon of gas you find you can go 26 miles, if you drive 20mph.
You can go 34 miles if you go 40mph and 32 miles if you go 50mph.
Find a quadratic function that models this data.
What is the best speed to go with this model?
:
Set up a set of coordinates, where x = speed, y = miles traveled on 1 gal of gas
Using the form y = ax^2 + bx (we don't need c here) find a and b
:
"you can go 26 miles, if you drive 20mph."
x=20, y=26
20^2a + 20b = 26
400a + 20b = 26
:
"32 miles if you go 50mph."
x=50, y=32
50^2a + 50b = 32
2500a + 50b = 32
:
multiply the first equation by 2.5, subtract from the above equation
2500a + 50b = 32
1000a + 50b = 65
------------------Subtraction eliminates b, find a
1500a = -33
a = 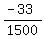
a = -.022
Find b, using the 1st equation
400(-.022) + 20b = 26
-8.8 + 20b = 26
20b = 26 + 8.8
20b = 34.8
b = 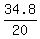
b = 1.74
:
The equation we are looking for:
y = -.022x^2 + 1.74x
;
Check this when,"You can go 34 miles if you go 40mph"
Replace x with 40 mph
y = -.022(40^2) + 1.74(40)
y = -35.2 + 69.6
y = 34.4 not quite 34 but the equation is very close
:
"What is the best speed to go with this model?"
Find the axis symmetry for this equation for max distance ; x=-b/(2a)
In this equation; a=-.022; b=1.74
x = 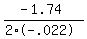
x = 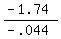
x = +39.545 mph, the speed for max distance
|
|
|