Question 422632: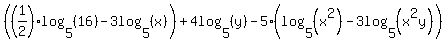 
I have no idea how to simplify this :( please help mee.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!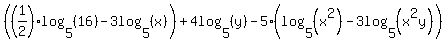
Reducing the number of terms by combining them is part of the process of simplifying. This reduction is often done by adding and subtracting like terms.
Like logarithmic terms have bases and arguments that are the same. For example in the expression:
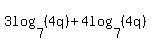
The logarithms have the same bases, 7, and the same arguments, 4q. So they are like terms and can be added. And exactly like 2x + 4x = 6x:
None of your terms are like terms. So we will not be able to add ot subtract any of them. However logarithms have some properties that provide an alternate way to combine logarithmic terms: 
These properties require that the bases are the same and the coeddicients (the numbers in front) to be 1's. All your terms have bases that are the same. But most of them do not have 1's in front. So we cannot use these properties, yet.
Fortunately there is another property of logarithms,  , that provides a way to "move" a coefficient "out of the way". The property let's us move a coefficient into the argument as its argument.
So what we are going to be doing is- Using the 3rd property on any logs that have a coefficient other than 1
- Using one of the first two properties to combine terms:
- We'll use the first property to combine terms that have a "+" between them
- We'll use the second property to combine terms that have a "-" between them
Starting with the third property:
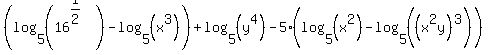
which we can simplify. Since 1/2 as an exponent means square root and since the square root of 16 is 4, the first argument becomes a 4. And we can use some rules for exponents,  and  to simplify the last argument:
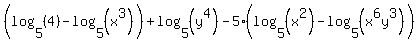
We can now use the second property on the first two terms and the last two terms:
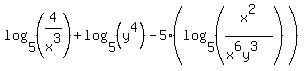
The fraction in the last argument simplifies:
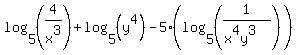
The only 5 that is not a base is in front of a set of parentheses. Before now the expression in those parentheses was more than a single logarithm. So we could not use the third property earlier. But now, since there is just a single logarithm, we can use the third property:
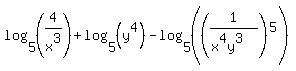
The last argument simplifies to:
Now we can use the first property on the first two logarithms:
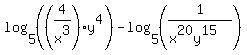
which simplifies to:
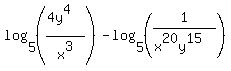
Next we use the second property to combine the remaining logarithms:
And we finish by simplifying the fraction in the argument. We will change this from a division of fractions to multiplying by the reciprocal:
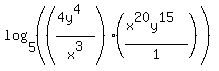
Multiplying the numerators and denominators we get:
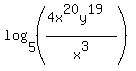
And last of all we reduce the fraction:
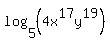
That's all there is to it! ;)
|
|
|
