|
Question 421778: use rational exponets to write ^3 sqrt8 * ^4 sqrt 5 as a single radical expression
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! If your expression is not

then please re-post your problem and use English to describe it since you don't seem to understand how to use mathematical notation in a way people can understand.
If your expression is

then- There are no square roots in this expression.
- The 3 and the 4 are not exponents! They are indices ("indexes") for the radicals. The index of a radical tells you what kind of root the radical is. The 3 on the first radical tells us that it is a 3rd (better known as cube) root. The 4 on the second radical tells us that it is a 4th root. (A radical without a visible index has an implied index of 2. IOW: A radical without a visible index is a 2nd (better known as square) root.
Since radicals of any kind are difficult to type, I recommend that in the future you use English to describe them. For example your expression could be described as
cube root of (8) * 4th root of (5)
Note how I used parentheses. Without them it would mean:
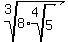
which i snot the same thing.
Back to your problem. Since  then then  . So you expression becomes: . So you expression becomes:
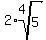
which is a "single radical" expression.
However we did not use rational exponents to find this answer. Using rational exponents is the hard way to do this problem because the first radical simplified so easily. If the first radical had not simplified so easily then rational exponents would be the only way to simplify to a single radical expression. So it is a technique your teacher should be asking you to learn and practice.
Here's a to your problem which uses rational exponents. First we must understand that cube roots and 4th roots can be expressed with radicals, as shown above, or with fractional/rational exponents. A cube root can be expressed as an exponent of 1/3 and a 4th root can be expressed as an exponent of 1/4. So your original expression, written with rational exponents is:
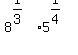
Next we want both factors to have the same exponents so we can use one of the properties of exponents,  , to multiply them together and have a single exponent. (This is how we are going to "merge" the two roots into one. To make the two exponents be the same we start by making the denominators the same (just like you do when adding fractions). The lowset common denominator is 12. Rewriting the exponents with denominators of 12 we get: , to multiply them together and have a single exponent. (This is how we are going to "merge" the two roots into one. To make the two exponents be the same we start by making the denominators the same (just like you do when adding fractions). The lowset common denominator is 12. Rewriting the exponents with denominators of 12 we get:
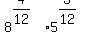
Next we factor out the numerators:
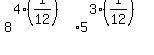
Then we use another property of exponents,  : :
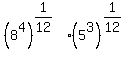
Since  and and  this becomes: this becomes:
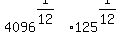
We now have the expression with the same exponents. Using the property mentioned earlier we get:

Now that we have the entire expression being raised to a rational exponent, we can switch back to radical form:

which simplifies to
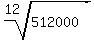
This may be the desired answer. But this will simplify further. (In fact we have already figured out (without using rational exponents) that it simplifies down to 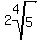 .) To simplify a 12th root we look for 12th power factors. Since .) To simplify a 12th root we look for 12th power factors. Since  there is a 12th power factor: there is a 12th power factor:

Using a property of radicals,  , to split this into two 12th roots: , to split this into two 12th roots:
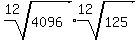
And the first root simplifies to 2:
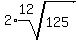
There are no 12th power factors in 125. But  and since 3 is a factor of 12 we can use some fancy juggling to simplify this: and since 3 is a factor of 12 we can use some fancy juggling to simplify this:
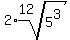
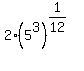
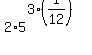
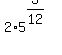

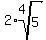
As I mentioned earlier, using rational exponents on this particular problem was the hard way to do it. But on other expressions using rational exponents is the only choice.
|
|
|
| |