Question 421190: Solve : (9)^y + 5 [(3)^y - 10] = 0
*Please answer as soon as possible. :) =)
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
When solving equations it is usually a good idea to start by simplifying each side of the equation. So we will start by using the Distributive Property to multiply on the left side:
After simplifying, identify the type of equation you have. The type of an equation determines the types of things you do to solve it. This is an exponential equation because the variable is in an exponent. Not only that, it is an exponential equation with multiple exponential terms,  and 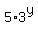 . With this kind of equation you either make the bases of the exponents equal, if possible, or you use logarithms. Since one base, 9, is a well-known power of 3, it will be easy to change the base of that term from 9 to 3:
The rule for exponents when raising a power to a power is to multiply the exponents. So the first term simplifies:
What's next? With this equation the "easy" solution is found by recognizing that the exponent on the first term is twice the exponent of the second term. This makes it an equation of "quadratic form". Equations of quadratic form can be solved with the same techniques as "regular" quadratic equations.
Until you have done enough of these quadratic form equations to get comfortable with them, it can be helpful to use a temporary variable. Just pick an unused variable and set it equal to the base to the lower exponent power. In this case:
Let 
Then 
Now substitute q and  into the equation:
This is clearly a quadratic equation. We can solve it by factoring (or by using the Quadratic Formula). This factors easily:
(q+10)(q-5) = 0
From the Zero Product Property we know that one of these factors must be zero. So:
q+10 = 0 or q-5 = 0
Solving these we get:
q = -10 or q = 5
We have solved for q. But we are not interested in solutions for q. We are interested in solutions for y. So we now substitute back in for the q's:
 or 
Now we solve these equations. Since a power of 3 can never be negative, there are no solutions to the first equation. So we solve just the second equation. This is another exponential equation but this one has just one exponential term. (So we have made progress!) With this type of equation, you want the exponential term isolated. Our exponential term is already all by itself on the left side so we don't have to do anything to isolate it. Next, if the solution is not obvious, you use logarithms. Since the power of 3 that results in 5 is not obvious we will use logarithms. (If the equation had been  then we would know the power of 3 that results in 9. It is a 2!)
Logarithms of any base can be used. But if you choose- a base that matches the base of the exponent, you will end up with a simpler expression.
- a base that your calculator "knows", like base 10 or base e (aka ln), then you will get an expression that will be easier to convert into a decimal approximation.
Going for the simpler expression we will use base 3 logarithms:
Next we use a property of logarithms,  , to move the exponent of the argument out in front of the logarithm. (It is this very property that is the reason we use logarithms. It allows us to move the exponent, where the variable is, out in front where we can then solve for the variable.) Using this property on our equation we get:
By definition  . (This is why matching the base of the logarithm to the base of the exponent gives us a simpler answer.) So this becomes:
This is an exact expression of the solution to your equation.
As I mentioned earlier, once you get used to these quadratic form equations thay get easier. Eventually you will no longer need to use a temporary variable. You will be able to see how to go directly from
to
to
 or 
etc.
|
|
|
