Question 42054: Find the largest three digit number which has exactly ten factors, including 1 and itself.
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! If any number has 'N' has 'r' prime number factors and can be expressed as
 
where  , ,  , , 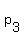 , ... are the prime factors and , ... are the prime factors and 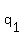 , , 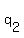 , , 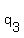 , .... are their respective indices. , .... are their respective indices.
For such a number N, the total number of factors (including 1 and itself) is given by 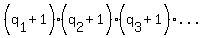 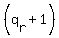 . .
Here total no. of factors = 10.
Hence, 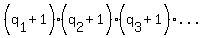 
As 10 itself has prime factors 2 and 5.
So the reqd. number must have only two prime factors such that the index of one of them is (2-1=) 1 and that of the other is (5-1=) 4.
So, 
As N has to be largest of all 3-digited number possible.
First, let us try with 
Let,  = 7. Then = 7. Then  > 1000. > 1000.
Let,  = 5. Then = 5. Then  < 1000 but < 1000 but  has to be atleast 2. So then N > 1000. has to be atleast 2. So then N > 1000.
Let,  = 3. Then = 3. Then  . Under this condition . Under this condition  (max) = 11 so N(max) = 891 < 1000. OK (max) = 11 so N(max) = 891 < 1000. OK
Let,  = 2. Then = 2. Then  . Under this condition . Under this condition  (max) = 61 so N(max) = 976 < 1000. OK (max) = 61 so N(max) = 976 < 1000. OK
Hence 976 is the largest 3-digit number with exactly 10 factors including (1 and itself).
These factors are: 1, 2, 4, 8, 16, 61, 122, 244, 488, 976.
|
|
|