Question 420125: For how many integers n is n/(20-n) the square of an integer?
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! We could assign k to be an integer such that  . Solve for n and you will get . Solve for n and you will get  --> -->  --> -->  . Here, the positive factors of 20 are 1,2,5,10,20, so k^2 can equal 0,1,4,9, or 19. This implies that k = {0,1,2,3} and n = 0, 10, 16, or 18. . Here, the positive factors of 20 are 1,2,5,10,20, so k^2 can equal 0,1,4,9, or 19. This implies that k = {0,1,2,3} and n = 0, 10, 16, or 18.
Another way just as effective is to brute-force the problem. Most math teachers recommend against this, but I will sometimes brute-force a problem if I know for sure the method will work, if I know I'm counting all possible cases, and if the method does not take too much time. Here, we know that n can only be between 0 and 20; otherwise, 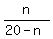 would be negative. would be negative.
|
|
|