Question 419848: Prove that the sum of the distances from any point in the interior of a equilateral triangle to each of the sides of the triangle is equal to the length of an altitude of that triangle.
Answer by richard1234(7193)   (Show Source):
You can put this solution on YOUR website! 
It's a little hard to draw here, but let x,y,z be the altitudes from D onto AB, BC, CA, respectively (segment x is perpendicular to AB, etc.). We know that the sum of the areas of the triangles ADB, BDC, CDA add up to the area of ABC, so
 where h is the altitude from C onto AB.
Since the triangle is equilateral,  and we can replace BC, CA with AB, without loss of generality.
We can multiply both sides by 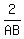 , cancelling out the AB and 2. Hence, we obtain
 , as desired.
|
|
|
