Question 419691: Solve equations for x. Check for extraneous solution. Round to three decimal places if needed.
5 plus 3e raised to the 3x power equals 12
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! I assume the equation is:
What you typed might also mean:
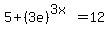
or
which are not the same thing as the first. If the second equation or third equation is actually correct, please re-post your problem if the solution below for the first equation does not help you figure it out. (If you re-post, then put parentheses around whatever expression has the exponent of 3x.)
We start by isolating the base and its exponent. So we subtract 5 from each side:
Now we divide by 3:
Now we use logarithms. Although any base of logarithm can be used, we will get the simplest expression if we match the base of the logarithm with the base of the exponent. So we will use base e, aka ln, logarithms:
Next we use one of the properties of logarithms,  , to move the exponent of the argument out in front. (It is the very property that is the reason we use logarithms. It allows us to move the exponent, where the variable is, to a location where can then solve for the variable.) Using this property we get:
Since ln(e) = 1 by definition (this is why base e logs give us a simpler expression) this becomes:
Dividing by 3 we get:
Since exponents can be any number, there is no chance for an "extraneous" solution. So this is an exact expression for the solution. For the requested decimal answer, get out your calculator, find ln(7/3), divide it by 3 and then round off the decimal to three places.
|
|
|
