Question 41948: If every person in our class shakes hands with every other perison in the class exactly once
(a) How many handshakes will have taken place if there are 22 studemts in the class
(b) If there were 35 students in the class, how many handshakes would there be?
(c) What if there were n people?
Found 2 solutions by psbhowmick, fractalier:
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! Suppose there were 'n' people.
Then each shook hands with (n-1) people.
So total number of handshakes = 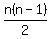
[Why divided by 2? The answer is whether person A shakes hand with person B or person B shakes hand with person A is immaterial as these two situations refer to a single handshake.]
For 22 and 35 students put n = 22 and 35 respectively and you will get 231 and 595 handshakes accordingly.
Answer by fractalier(6550)   (Show Source): (Show Source):
You can put this solution on YOUR website! We can see the pattern by looking at how many handshakes each person makes...
The first person can shake 21 hands, the second person can shake 20 hands, since they already shook hands with person #1, the 3rd person does 19, the 4th 18, and so on...
The sum of these 21 numbers is n(n+1) / 2 = 21(22) / 2 = 231.
In terms of the 22 people, it becomes (n-1)n / 2, and that is the general expression you need in part c...
Part b) Given there are 35 people, the number of shakes is 34(35) / = 17(35) = 595 handshakes...
|
|
|