SOLUTION: I just can't seem to get the simplifying of rational expressions. Can you show me how to do these? 1: (x^2+16/2x+8) / ((x-4)^2/8x-32) 2: (1/3x)/(5/6y) 3: ((2/y)-1)/((3/x)

Algebra ->  Rational-functions -> SOLUTION: I just can't seem to get the simplifying of rational expressions. Can you show me how to do these? 1: (x^2+16/2x+8) / ((x-4)^2/8x-32) 2: (1/3x)/(5/6y) 3: ((2/y)-1)/((3/x)      Log On


   

Question 419145: I just can't seem to get the simplifying of rational expressions. Can you show me how to do these?
1: (x^2+16/2x+8) / ((x-4)^2/8x-32)
2: (1/3x)/(5/6y)
3: ((2/y)-1)/((3/x)+1)
I'm lost.
Thank you.
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
First, please put multiple term numerators and/or denominators in parentheses. It will help keep the expression clear and clearly written problems are more likely to get a response from the tutors.

I am going to do these starting with the easiest and ending with the hardest:
2: 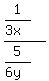%281%2F%283x%29%29%2F%285%2F%286y%29%29
Here we have a fraction divided by a fraction. Just as you learned long ago, we divide fractions by multiplying by the reciprocal of the divisor. Changing this expression into multiplying by the reciprocal we get:
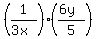
%281%2F%283x%29%29%2A%28%286y%29%2F5%29
Now that it is a multiplication of fractions, we will cancel factors before we multiply. (This is an optional but highly recommended step. And while it will not make much difference with this expression, it will become very important in one of your other problems.)
%281%2F%283x%29%29%2A%28%282%2A3y%29%2F5%29
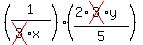
%281%2F%28cross%283%29x%29%29%2A%28%282%2Across%283%29y%29%2F5%29
leaving:
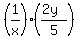
%281%2Fx%29%2A%28%282y%29%2F5%29
Now we multiply:
%282y%29%2F%285x%29

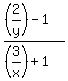
3: %28%282%2Fy%29-1%29%2F%28%283%2Fx%29%2B1%29
This one is another division. But this time we have fractions within the fractions. I find that ihese are handled best by eliminating the "little" fractions within the big fraction, first. This can be done by multiplying the numerator and denominator of the "big" fraction by the lowest common denominator (LCD) of all the "little" denominators. The "little" denominators are y and x. The LCD of these two is y*x. Multiplying the numerator and denominator of the "big" fraction by y*x:
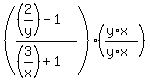
%28%28%282%2Fy%29-1%29%2F%28%283%2Fx%29%2B1%29%29%28%28y%2Ax%29%2F%28y%2Ax%29%29
In both the numerator and denominator we will use the Distributive Property to {multiply:

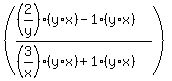
All the "little" denominators cancel:

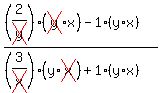
leaving
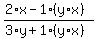
%282%2Ax-1%2A%28y%2Ax%29%29%2F%283%2Ay%2B1%2A%28y%2Ax%29%29
which simplifies to:
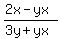
%282x-yx%29%2F%283y%2Byx%29
The only thing left is to try to reduce the fraction. To reduce it properly we have to factor the numerator and denominator and see if they have any factors in common. Even though there is a GCF we can factor in both the numerator and denominator, we do not end up with any factors in common. So this fraction will not reduce.

1: 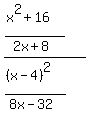%28%28x%5E2%2B16%29%2F%282x%2B8%29%29+%2F%28%28%28x-4%29%5E2%29%2F%288x-32%29%29
This one, like the first one, is a division of fractions. So we will change ii into a multiplication by the reciprocal:
%28%28x%5E2%2B16%29%2F%282x%2B8%29%29+%2A%28%288x-32%29%2F%28%28x-4%29%5E2%29%29
As mentioned earlier, it is a very good habit to cancel common factors before actually multiplying. This is especially true here. After all, who wants to multiply these two fractions as they are right now? To cancel common factors we must of course know what the factors are. So we start by factoring each numerator and denominator as much as possible. The first numerator is a sum of squares and will not factor. The second denominator is already in factored form. But the other numerator and other denominator will factor:
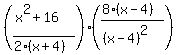
%28%28x%5E2%2B16%29%2F%282%28x%2B4%29%29%29+%2A%28%288%28x-4%29%29%2F%28%28x-4%29%5E2%29%29
To make things even clearer I am going to factor that 8 and write the second denominator without an exponent so we can see what gets canceled:

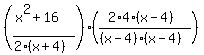
Now we can cancel:

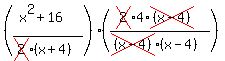
leaving:
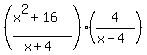
%28%28x%5E2%2B16%29%2F%28x%2B4%29%29%2A%284%2F%28x-4%29%29
This, you must agree, looks a lot easier to multiply. And not only that we will not have to reduce the fraction afterwards because we have already done all the reducing! Multiplying this out we use the Distributive Property on top and either FOIL or the %28a%2Bb%29%28a-b%29+=+a%5E2-b%5E2 pattern on the bottom. Both will work but I prefer using patterns:
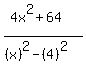
%284x%5E2%2B64%29%2F%28%28x%29%5E2+-+%284%29%5E2%29
which simplifies to:
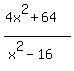
%284x%5E2%2B64%29%2F%28x%5E2+-+16%29
As much as this looks like something will cancel, we have already seen the factors and there are no common ones to cancel. This is the simplified solution.