Question 4186: Okay. I know I asked this already, and I thank you longjohnsilver for your post; but quite frankly, that makes no sense. I need some kind of basic formula for annual interest. I remember learning it, but can't recall it all.
A BOND PAYS 12% ANNUAL INTEREST COMPOUNDED CONTINUOUSLY. IF $10,000 IS INVESTED INITIALLY, WHEN WILL THE BOND BE WORTH $30,000? ROUND TO NEAREST YEAR.
Found 2 solutions by longjonsilver, rapaljer:
Answer by longjonsilver(2297)   (Show Source): (Show Source):
You can put this solution on YOUR website! OK, try this:
start with 10000.
After 1 year you have 10000*1.12 = whatever.
After another year, you have whatever*1.12 = something.
After a third year, you have something*1.12 = value
After a fourth year, you have a value*1.12 = figure
etc etc.
Work that out until you reach 30,000. It will be 10 years.
Mathematically, what we have is:
after year 1: 10000*1.12
after year 2: 10000*1.12*1.12
after year 3: 10000*1.12*1.12*1.12
after year 4: 10000*1.12*1.12*1.12*1.12
after year 5: 10000*1.12*1.12*1.12*1.12*1.12
etc
which can be written as:
after 1 year : 10000*1.12^1
after 2 years: 10000*1.12^2
after 3 years: 10000*1.12^3
after 4 years: 10000*1.12^4
after 5 years: 10000*1.12^5
... after n years: 10000*1.12^n and this has to be 30000. So:

 . Taking logs: . Taking logs:
nlog1.12 = log3
n=log3/log1.12
n=9.694
so n=10 years
jon
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! I was thinking to use the formula for interest compounded continuously

In this formula, A=$30,000, P=$10,000, r=.12, and of course t is the unknown in years.
Substituting, this gives you:

Divide both sides by 10000 to obtain

Take the ln of both sides


Divide both sides by .12, and the answer I get is 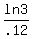
I don't have my calculator with me, but I think that is approximately 9.185 years, which rounds off to the nearest year of 9.
What do you think?
R^2
Seminole Community College
Sanford, Florida
|
|
|