Question 418437: A passenger train travels 55 miles per hour, and a freight train travels 31 miles per hour. When they run on parallel tracks in the same direction, they clear each other in 70 seconds. When they are traveling in the same direction on the parallel tracks and the engines are exactly opposite each other, they clear each other in 25 seconds. If the freight train is the longer, find the length of each train.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A passenger train travels 55 miles per hour, and a freight train travels 31 miles per hour.
:
Change speeds to ft/sec
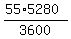 = 80.667 ft/sec, for the pass train = 80.667 ft/sec, for the pass train
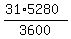 = 45.667 ft/sec, for the freight = 45.667 ft/sec, for the freight
:
When they run on parallel tracks in the same direction, they clear each other in 70 seconds.
The difference in their speed: 80.667 - 45.667 = 35 ft/sec which is the speed relationship between the two trains
We can use this information to find the total length of the two trains
:
70(35) = 2450 ft total length of the two trains
:
When they are traveling in the same direction on the parallel tracks and the
engines are exactly opposite each other, they clear each other in 25 seconds.
If the freight train is the longer, find the length of each train.
25(35) = 875 ft is the pass train
and
2450 - 875 = 1575 ft is the freight
|
|
|