Question 417664: 2^(x) = 3^(x-1)
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
Solving equations where the variable is in an exponent is usually done with logarithms. The base of the logarithm used is not really important. Any base will work. However:- Choosing a base for the logarithm that matches the base of one of the exponents will result in a simpler expression for the answer.
- Choosing a base for the logarithm that your calculator "knows", like base 10 or base e (aka ln), will make it easier to get a decimal approximation.
So with your equation, choosing base 2 or base 3 logarithms will give us a simpler expression and choosing base 10 or base e logarithms will give us a more complex expression but one that will be easier to turn into a decimal approximation. I will use them all.
Starting with base 2 logarithms:
Now we use a property of logarithms,  , which allows us to move the exponent of the argument of a logarithm out in front as a coefficient. It is this very property that is the reason we use logarithms on equations like this. The property gives us a way to move the exponent, where the variable is, to a location where we can then solve for the variable. And this property, which works for any base of logarithm, is also the reason we can choose any base of logarithm.
Using this property on both sides of our equation we get:
which simplifies to:
Since  by definition this further simplifies to:
(This log that turns into a 1 is the reason we get a simpler expression when using a base of logarithm that matches one of the bases of the exponents.)
We can now solve for x. We start by gathering the x terms on one side of the equation and the other terms on the other side of the equation. Subtracting 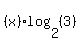 from each side we get:
Factoring out x we get:
Dividing by  we get:
This is an exact solution for your equation.
If we use base 3 logs instead...
The steps are all the same except a different logarithm turns into a 1 so I will not provide much explanation:
The log on the right becomes 1:
Another exact expression for the solution.
If we use ln instead...
The steps are the same except no logarithms become a 1. (This is why we get a more complex expression.)
Multiplying out the right side:
If we use base 10 log instead...
The steps are exactly the same as those for ln. So we get:
Although our four solutions:
and
look different they are all exact, correct solutions to your equation. If you turned them all into decimal approximations you would find that they all work out the same. (To turn the base 2 or base 3 log solutions into decimals, you must use the change of base formula,  , to convert the base 2 or 3 logs into base 10 or base e logs so you can then use your calculator.)
|
|
|
