|
Question 417591: what is the cubed root of 72x to the fifth power y to the ninth power ?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Simplifying cube roots involves finding perfect cube factors (other than 1), if any, of the radicand. (The expression inside a radical is called the radicand.)
Since  and since 8 is a factor of 72 we do have a perfect cube factor in 72. and since 8 is a factor of 72 we do have a perfect cube factor in 72.
For the variable factors, 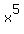 and and  , they will have perfect cube factors if their exponents are greater than or equal to 3, Factoring the radicand into as many perfect cube factors as possible we get: , they will have perfect cube factors if their exponents are greater than or equal to 3, Factoring the radicand into as many perfect cube factors as possible we get:

For reasons you will see shortly, like to use the Commutative Property to rearrange the order of the factors so that all the perfect cube factors are in front:

Now we use a property of radicals,  , to put the prefect cube factors into their own cube roots. (The factors that are not perfect cubes all go into a single cube root.): , to put the prefect cube factors into their own cube roots. (The factors that are not perfect cubes all go into a single cube root.):
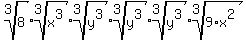
The cube roots of the perfect cubes simplify:
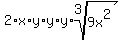
which simplifies to:
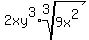
This is the simplified expression. Notice that the remaining cube root is at the end of the expression. This is how expressions like this are usually written. By having the radical at the end there is no possible confusion as to what is inside the radical and what is outside the radical. If we use 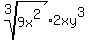 , especially if we write this instead of typing it, it may not be clear what is inside and what is outside the radical. By rearranging the factors earlier so that all the perfect cube factors were in front, we ended up with the expression as we wanted it -- with the radical at the end. , especially if we write this instead of typing it, it may not be clear what is inside and what is outside the radical. By rearranging the factors earlier so that all the perfect cube factors were in front, we ended up with the expression as we wanted it -- with the radical at the end.
|
|
|
| |