Question 417085: Two trains, one 350 feet long, the other 450 feet long, on parallel tracks, can pass each other completely in 8 seconds when moving in opposite directions. When moving in the same direction, the faster train completely passes the slower one in 16 seconds. Find the speed of the slower train
Please help me with the steps,
Thank you!
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! Two trains, one 350 feet long, the other 450 feet long, on parallel tracks, can
pass each other completely in 8 seconds when moving in opposite directions.
When moving in the same direction, the faster train completely passes the slower one in 16 seconds. Find the speed of the slower train
:
let f = speed of the faster train (in ft/sec)
let s = speed of the slower train
:
The total distance covered when trains pass each other: 450 + 350 = 800 ft
:
Two distance equations; dist = time * speed
:
opposite directions,
8(f + s) = 800
simplify, divide by 8
f + s = 100
:
Same direction
16(f - s) = 800
Simplify, divide by 16
f - s = 50
:
Add these two simplified equations
f + s = 100
f - s = 50
--------------addition eliminates s find f
2f = 150
f =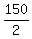 
f = 75 ft/sec speed of the faster train
:
Find s using the equation f + s = 100
75 + s = 100
s = 100 - 75
s = 25 ft/sec is the speed of the slower train
Convert to mph
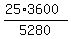 = 17.045 mph is the slow train
:
:
Check solution in the original opposite direction equation
8(75 + 25) = 800
|
|
|
