SOLUTION: 7^(3x) = 20

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: 7^(3x) = 20      Log On


   

Question 415912: 7^(3x) = 20
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
7%5E%283x%29+=+20
Solving equations where the variable is in an exponent is usually done in either of two ways:
  • Rewriting the equation so that both sides of the equation are powers of the same number. This cannot always be done but the solution is easier this way.
  • Using logarithms.

7 is not a power of 20 (a least not a power I know), 20 is nota power of 7 and 20 and 7 are not both powers of some third number. So the first option is not available to us. We must use logarithms.

Logarithms of any base can be used. However
  • Using a base of logarithm which matches the base of the exponent will lead to a simpler answer. In this problem, the base of the exponent is 7. So using base 7 logarithms will lead to the simplest answer.
  • Using a base of logarithm that your calculator "knows" (usually base 10 and/or base e (aka ln)) will lead to answer that will be easier to turn into a decimal approximation.

We'll start with base 7 logarithms:
log%287%2C+%287%5E%283x%29%29%29+=+log%287%2C+%2820%29%29
Next we use a property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, which allows us to take the exponent of the argument and move it out in front as a coefficient. (It is this very property that is the reason we use logarithms on these equations. It allows us to move the exponent, where the variable is, to a location where we can then solve for that variable.) Using the property on the left side we get:
%283x%29log%287%2C+%287%29%29+=+log%287%2C+%2820%29%29
And, since log%287%2C+%287%29%29+=+1 be definition (This is why choosing base 7 logs gives us the simplest expression.), this becomes:
3x+=+log%287%2C+%2820%29%29
Now we divide by 3:
x+=+log%287%2C+%2820%29%29%2F3
This is an exact solution for your equation. To convert this into a decimal approximation, use the change of base formula, log%28a%2C+%28p%29%29+=+log%28b%2C+%28p%29%29%2Flog%28b%2C+%28a%29%29, to convert the base 7 log into an expression of base 10 or base e logarithms so you can use your calculator.

Now we'll use base e logarithms. The steps are the same (except one of the logarithms will not turn into a 1) so I will not explain them again.
7%5E%283x%29+=+20
ln%287%5E%283x%29%29+=+ln%2820%29
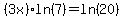
%283x%29ln%287%29+=+ln%2820%29
Dividing by 3ln(7) ...
x+=+ln%2820%29%2F%283ln%287%29%29
This is another exact expression for the solution to your equation. It is not as simple as the base 7 solution but it is easier to convert into a decimal approximation.