Find the equation for a parabola with its focus at (5,0) and with
directrix x=-5.
Here is its focus, the point F(5,0), and its directrix, the green
line below.
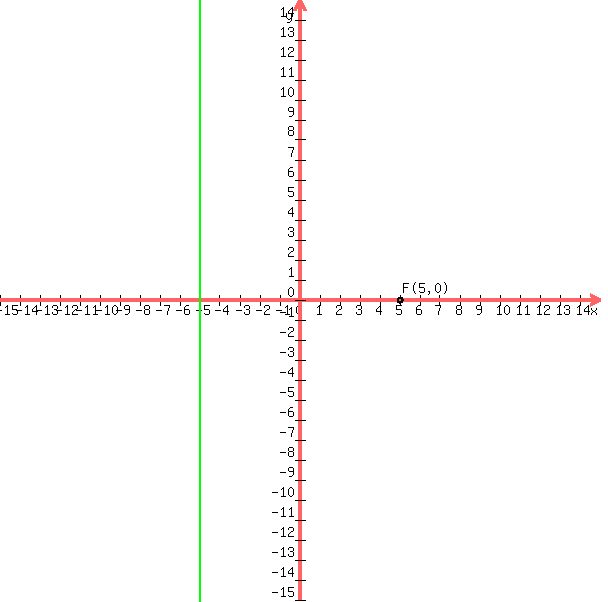The vertex of a parabola is half-way between the focus point and the
directrix line. Looking at the graph, that puts the vertex at the origin
V(0,0). p is the distance from the vertex to the focus, taken as a positive
number if the parabola is to open to the right and p is taken as a negative
number if the parabola is to open to the left.
This one opens to the right, so p is taken positive as 5, the distance
between the vertex and the focus, which is also half of the distance between
the focus and the directrix. So its equation is
(y - k)² = 4p(x - h)
and since the vertex is (h,k) = (0,0) and p = 5, that simplifies to
(y - 0)² = 4*5(x - 0)
y² = 20x
That's the equation you wanted
To finish the graph we constract a square on each side of the line
that goes from the focus through the vertex to the directrix, like this:
Then we can sketch in the parabola through the vertex and the right
uppermost and lowermost corners of those two squares:
Edwin
