Question 414707: I need to combine the following into one log (base 3)
ln{x{log (base 1/2)(2/(sqrt(2)))}} + log {(base 2)(5x^3)} + 3
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 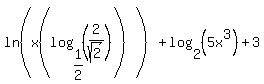
First, let's simplify the expression. Then we will try to combine it into a single base 3 logarithm. First, let's look at 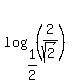 . The 1/2, the 2 and the . The 1/2, the 2 and the  are all powers of 2. So if we use the change of base formula to change the base to 2, this log will simplify greatly. The change of base formula is: are all powers of 2. So if we use the change of base formula to change the base to 2, this log will simplify greatly. The change of base formula is:  . Using this pattern on . Using this pattern on 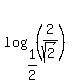 we get: we get:
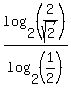
In the numerator we can use a property of logarithms,  : :

Each of these three logs can be simplified because each of the arguments are "known" powers of 2 ( , ,  and and  . Replacing each of the logs with these values we get: . Replacing each of the logs with these values we get:
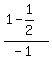
which simplifies as follows:
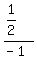

So  . Replacing . Replacing 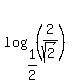 with -1/2 in the original expression we get: with -1/2 in the original expression we get:

which simplifies to
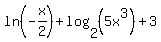
At this point I'd like to point out that this expression and, therefore, your original expression are invalid. This is true because arguments to all logarithms must be positive. In order the the -x/2 to be positive, then x must be negative. But if x is negative, then the other argument, 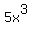 , would be negative. So there is no way for both arguments to be positive! So these expressions are invalid. , would be negative. So there is no way for both arguments to be positive! So these expressions are invalid.
This, and the complexity of the final answer lead me to suspect that either the problem was defined incorrectly or there is an error in how you posted it.
Proceeding as if we didn't know that the expression is invalid...
We are now ready to start writing the expression in terms of base 3 logs. For the two logarithms we can use the change of base formula. For the "3" at the end we will use the fact that  so so  . So we can replace the 3 with . So we can replace the 3 with  : :

To combine these three terms together into a single logarithm we will be using a property of logarithms:  . This property requires that the logarithms not be in a fraction. There is no property that directly addresses the issue of the fractions (i.e. divisions). But there is a property that handles coefficients (i.e. multiplication): . This property requires that the logarithms not be in a fraction. There is no property that directly addresses the issue of the fractions (i.e. divisions). But there is a property that handles coefficients (i.e. multiplication):  . So we will be able to combine the logarithms if we turn the divisions into multiplications and then use this property to move the coefficient into the argument as its exponent. . So we will be able to combine the logarithms if we turn the divisions into multiplications and then use this property to move the coefficient into the argument as its exponent.
Checking the two fractions into multiplying by the reciprocal we get:
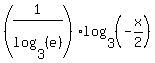
Now we can use the property to move the coefficients:
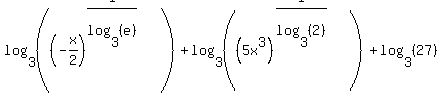
Now we can use the property to combine the logarithms: 
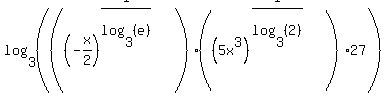
A single albeit complex base 3 logarithm.
|
|
|