SOLUTION: If you add consecutive odd integers beginning with 1, the sum will always be a square. Why is this true? How do I prove this algebraically?

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: If you add consecutive odd integers beginning with 1, the sum will always be a square. Why is this true? How do I prove this algebraically?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 413850: If you add consecutive odd integers beginning with 1, the sum will always be a square. Why is this true? How do I prove this algebraically?
Answer by bayners123(12) About Me  (Show Source):
You can put this solution on YOUR website!
If you write out a sequence with even intervals between the values of the numbers, then to find the sum of the sequence you can find the average and multiply by the number of terms you have. As the numbers are evenly placed, to find the average you can just add the last and first and then divide by 2.
In this case that means you have the first term, 1, and the last term which will be 2n-1 for a series with n numbers in it. This makes the average 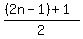%28%282n-1%29%2B1%29%2F2
which is just n.
Now to find the sum, just multiply the average, n, by the number of terms, also n, to find the sum of the series is, as anticipated, n%5E2