Question 413817: Can I get validation on my first part of the problem and help with the second half. I would greatly appreciate it.
A gargae door opener has a sequence of 10 switches, each switch has 3 positions (0,1,2).
a.) how many codes are possible with these switches.
C(10,3)= 720
b.)how many of these codes have exactly 4 twos and exactly 4 ones in them?
thanks,
Gina
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! a: 10C3 is incorrect. This is partially because 10C3 implies that you're choosing from ten switches or positions, etc. For this problem, it helps to realize that the order of the switches is relevant. There are three possibilities for each switch, so the total number of codes is  . .
b: If such a code has four 2's and four 1's, it must have exactly two 0's. It suffices to find the number of ten-digit codes with these properties. There are 10! ways to arrange the switches (note that the digits are already determined and we have to arrange them, this is why we use factorial). However, since the 2's are indistinguishable from each other, we divide by 4!, since the 10! assumes the 2's are different. Similarly, we divide by 4! to account for the 1's and 2! for the 0's. The number of codes is 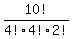 . .
|
|
|