Find a linear function h such that h(-1)=-5 and h(7)=-6. What is h(3/2)?
First you interpret it as this problems:
Find the equation of the line that passes through the two points
(-1,-5) and (7,-6).
Use the slope formula:
y2 - y1 (-6) - (-5) -6 + 5 -1
m = ---------- = -------------- = -------- = ----- =  x2 - x1 7 - (-1) 7 + 1 8
Then use the point-slope formula:
y - y1 = m(x - x1)
y - (-5) =
x2 - x1 7 - (-1) 7 + 1 8
Then use the point-slope formula:
y - y1 = m(x - x1)
y - (-5) =  (x - (-1) )
y + 5 =
(x - (-1) )
y + 5 =  (x + 1)
y + 5 =
(x + 1)
y + 5 =  x -
x -  y =
y =  x -
x -  - 5
y =
- 5
y =  x -
x -  -
- 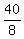 y =
y =  x -
x - 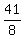 Now replace y by h(x)
h(x) =
Now replace y by h(x)
h(x) =  x -
x - 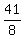 That's the first part.
That's the first part.
What is h( )?
)?
Substitute  for x in
h(x) =
for x in
h(x) =  x -
x - 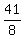 h(
h( ) =
) = 
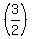 -
- 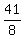 h(
h( ) =
) = 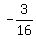 -
- 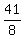 h(
h( ) =
) = 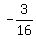 -
- 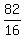 h(
h( ) =
) = 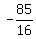 Edwin
Edwin