SOLUTION: can anyone help me solve the following log equation: Solve for x: 2^(x-1) = 3^(2x-1)

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: can anyone help me solve the following log equation: Solve for x: 2^(x-1) = 3^(2x-1)      Log On


   

Question 412938: can anyone help me solve the following log equation:
Solve for x:
2^(x-1) = 3^(2x-1)
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
2%5E%28x-1%29+=+3%5E%282x-1%29
Solving equations where the variable is in an exponent can be done in a couple of ways:
  • If possible, rewrite the equation so that each side is a power of the same number.
  • Use logarithms.

Since 2 and 3 are prime they share no common factors (other than 1) and so it will not be simple to write each side as powers of the same number. So we will use logarithms. Any base of logarithm can be used. However,
  • A simple expression will result if we choose to use a base that matches the base of one of the exponential terms. In this case we would choose base 2 or base 3 logarithms to get the simplest expression.
  • If you know or think you may want a decimal approximation for the answer, then choosing a base of logarithm thet your calculator "knows", like base 10 or base e (aka ln), would be a good choice
  • Any other choice of base will still work but it will result in a more complex expression and/or an expression that will be more difficult to turn into a decimal approximation.

Let's look at using base 2 logarithms. Finding the base 2 logarithm of each side we get:
log%282%2C+%282%5E%28x-1%29%29%29+=+log%282%2C+%283%5E%282x-1%29%29%29
Next we can use a property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, which allows us to move an exponent of the argument of a logarithm outr in front. (It is thie very property that is the reason we use logarithms on problems like this. It allows us to move the exponent, where the variable is, to a location where we can now solve for the variable.) Using the property on both sides of the equation we get:
%28x-1%29log%282%2C+%282%29%29+=+%282x-1%29log%282%2C+%283%29%29
By definition, log%282%2C+%282%29%29+=+1. (This is why base 2 or base 3 logarithms give us the simplest expression for an answer.) So this becomes:
%28x-1%29%2A1+=+%282x-1%29log%282%2C+%283%29%29
or just
x-1+=+%282x-1%29log%282%2C+%283%29%29
Now we solve for x. First we simplify the right side, using the Distributive Property:
x-1+=+2%28log%282%2C+%283%29%29%29x-log%282%2C+%283%29%29%29
Next we gather the x terms on one side and the "non-x" terms on the other side of the equation. Subtractin x fron each side and adding log%282%2C+%283%29%29 we get:
log%282%2C+%283%29%29-1+=+2%28log%282%2C+%283%29%29%29x+-+x
Factoring out x on the right side we get:
log%282%2C+%283%29%29-1+=+x%282log%282%2C+%283%29%29+-+1%29
And last of all we divide both sides by 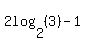2log%282%2C+%283%29%29+-+1:
%28log%282%2C+%283%29%29-1%29%2F%282log%282%2C+%283%29%29+-+1%29+=+x
This is an exact expression for the solution to your equation. If you need a decimal approximation, then you a) should have used base 10 or base e logs instead; or b) use the change of base formula to convert the logarithms above into base 10 or base e logarithms.

If we chose base 3 logarithms instead... (The steps are all the same as above except a different logarithm turns out to be 1 so I will not provide explanations.)
2%5E%28x-1%29+=+3%5E%282x-1%29
log%283%2C+%282%5E%28x-1%29%29%29+=+log%283%2C+%283%5E%282x-1%29%29%29
%28x-1%29log%283%2C+%282%29%29+=+%282x-1%29log%283%2C+%283%29%29
%28x-1%29log%283%2C+%282%29%29+=+2x-1
x%2Alog%283%2C+%282%29%29-log%283%2C+%282%29%29+=+2x-1
x%2Alog%283%2C+%282%29%29-2x+=+log%283%2C+%282%29%29+-1
x%2A%28log%283%2C+%282%29%29-2%29+=+log%283%2C+%282%29%29+-1
x+=+%28log%283%2C+%282%29%29+-1%29%2F%28log%283%2C+%282%29%29-2%29

If we chose base e logarithms instead... (The steps are all the same as above except no logarithm turns out to be 1 so I will not provide explanations.)
2%5E%28x-1%29+=+3%5E%282x-1%29
ln%282%5E%28x-1%29%29+=+ln%283%5E%282x-1%29%29
%28x-1%29ln%282%29+=+%282x-1%29ln%283%29
x%2Aln%282%29-ln%282%29+=+2x%2Aln%283%29-ln%283%29
ln%283%29-ln%282%29+=+2x%2Aln%283%29-x%2Aln%282%29
ln%283%29-ln%282%29+=+x%282ln%283%29-ln%282%29%29
%28ln%283%29-ln%282%29%29%2F%282ln%283%29-ln%282%29%29+=+x
If we chose base 10 logarithms instead we would end up with:
%28log%28%283%29%29-log%28%282%29%29%29%2F%282log%28%283%29%29-log%28%282%29%29%29+=+x

All four solutions, although they look different, are correct and exact expressions for the solution to your equation. The last two, with the base e or base 10 logarithms, are more complex but easier to turn into decimal approximations.