Question 411433: Solve equation and inequality. Use set builder notation or interval notation to write solution sets to the inequalities.
(a) 18x^2 + 9x - 20 = 0
(b) 18x^2 + 9x - 20 (-/=)0
(c) 18x^2 + 9x - 20 (+/=)0
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
To solve this equation we factor it (or use the Quadratic Formula). Factoring it we get:
(6x-5)(3x+4) = 0
From the Zero Product Property we know that one of these factors must be zero. So:
6x-5 = 0 or 4x+3 = 0
Solving each of these we get:
 or or 
To solve the inequalities we will use the answers to the equation. When  the factor (6x-5) is zero. When x is greater than 5/6, the factor will be larger than zero. (IOW: positive). And when x is less than 5/6 the factor willbe smaller than zero (negative). Using the same logic on the other factor we find that when x is larger than -4/3 the (4x+3) factor will be positive and when x is smaller than -4/3, that factor will be negative. the factor (6x-5) is zero. When x is greater than 5/6, the factor will be larger than zero. (IOW: positive). And when x is less than 5/6 the factor willbe smaller than zero (negative). Using the same logic on the other factor we find that when x is larger than -4/3 the (4x+3) factor will be positive and when x is smaller than -4/3, that factor will be negative.
Now let's put this together. Think of a number line with the numbers -4/3 and 5/6 plotted. These two points divide the number line into three parts:- The part to the left of -4/3
- The part to the right of 5/6
- The part between -4/3 and 5/6
Let's analyze what each factor, (6x-5) and (4x+3), will be in each of these parts of the number line:- For x's to the left of -4/3, both factors will be negative. And since a negative times a negative is positive, (6x-5)(4x+3) will be positive.
- For x's to the right of 5/6, both factors will be positive. And since a positive times a positive is positive, (6x-5)(4x+3) will be positive.
- In between -4/3 and 5/6, (4x+3) will be positive and (6x-5) will be negative. And since a positive time a negative is negative, (6x-5)(4x+3) will be negative.
So we have found that if
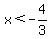 or or 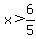
then (6x-5)(4x+3) will be positive. If we include the values that make the factors zero we get:
 or or 
This is the solution to 
In set notation this is {x |  or or  } }
And if
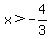 and and 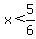
then (6x-5)(4x+3) will be negative. If we include the values that make the factors zero we get:
 and and 
This is the solution to 
In set notation this is {x |  and and  } or } or
{x |  } }
|
|
|