Question 41021: An infinite geometric series has 1 and 1/5 as its first two terms: 1,1/5,1/25,1/125,..... What is the sum, S, of the infinite series?
a)1/25
b)1/4
c)1
d)5/4
Found 3 solutions by checkley71, mszlmb, fractalier:
Answer by checkley71(8403)   (Show Source):
You can put this solution on YOUR website! JUST ADDING THE FIRST 2 TERMS WE GET 1.2 THEREFORE THE A,B,C ANSWERS ARE WRONG.
THE 5/4 ANS. IS = 1.25 THEREFORE IT IS THE CORRECT ANSWER.
Answer by mszlmb(115)  (Show Source):
You can put this solution on YOUR website! I LOVE infinite series.
ok so 1+1/5+1/25+1/125+1/625...
1+.2+.04+.008+.0016
or 1+(1*2)/10+(1*4)/100+(1*8)/1000...
or 1+...
we have 1/5+1/25=6/25+1/125=31/125+1/625=156/625 and so on
so y=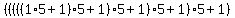
or, ignoring the order of whatever its called,
we add one and multiply by 5 over and over again, infinitely, over
0+1*5+1*5+1*5...
_____________
5(5)(5)(5)(5)
yielding 
or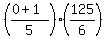 
ok forget all of that, a lot of it is wrong. But be ready to refer to it. don't worry if it made no sense.
now im very sorry, i feel quite childish in terms of intellect; perhaps you can solve it from here..
I got  ...:P I can't solve it anymore!
I do, however, feel like much less of a mathematical amateur telling you that the answer is obviously, of the four choices listed above, 5/4, because its the only number higher than one, and seeing as how this infinite series is 1+ something.. well, you can make the connection:)
I would REALLY appreciate it if you could perhaps teach me by way of email how to get the solution when you do
yours truly, <-)))><(((->
sorry about all that, i worked on it today..here's what iv come up with..
so we have 1+.2+.04+.008 etc.
Do you see the pattern, again, of *2 and *5?
This can be expressed as 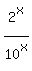 . That's to get any the xth number (ie the 5th number is 32/100000, or .000032; try it.)
Of course, this is not what we want, we want  when  ; E, representing sigma, means the addition of all of the following. By E[N] I mean sigma of all N, positive integers. (E[n]{1,2,3.4,5}=8)
we're basically looking for all solutions for 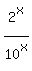given x=N (positive integer).
this can also be expressed as E[n]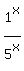 ; I can simplify it no further as of now.
Again, it is obvious the answer is 5/4 because it is the only choice over 1, an easy choice considering the question is 1+something.
I checked, and it really does equal 5/4; I just can't find how to get there :P
good luck and if u get the process email me ;)
Answer by fractalier(6550)  (Show Source):
You can put this solution on YOUR website! The formula for finding the sum of an infinite geometric series is
S = a1 / (1 - r)
where a1 is the first term and r is the common ratio...here those are 1 and 1/5, respectively...plugging in we get
S = 1 / (1 - 1/5) =
S = 1 / (4/5) =
S = 5/4
Choice D.
|
|
|
