Use the rational roots therm to list all the possible rational roots for the equation then find all the roots : f(x) = x³ - 2x² - 17x + 10
All the possible rational roots have numerators which are divisors
of 10, positive or negative, and whose denominators are the divisors of
the coefficient of x³, which is 1. Since 1 has only 1 divisor, 1, the
only possible roots are ± the divisors of 10.
±1, ±2, ±5, ±10
Try 1
1|1 -2 -17 10
| 1 -1 -18
1 -1 -18 -8
No, 1 is not a root because we get -8
on the bottom right as a remainder, not 0.
-1|1 -2 -17 10
| -1 3 14
1 -3 -14 24
No, -1 is not a root because we get 24
on the bottom right as a remainder, not 0.
2|1 -2 -17 10
| 2 0 -34
1 0 -17 -24
No, 2 is not a root because we get -24
on the bottom right as a remainder, not 0.
-2|1 -2 -17 10
| -2 8 18
1 -4 -9 28
No, -2 is not a root because we get 28
on the bottom right as a remainder, not 0.
5|1 -2 -17 10
| 5 15 -10
1 3 -2 0
Yes!! Finally!! 5 is a root because we get 0
on the bottom right.
So we have now factored the polynomial
f(x) = x³ - 2x² - 17x + 10
as
f(x) = (x - 5)(x² + 3x - 2)
The trinomial in the parentheses does not factor,
so we set each factor = 0
Setting the first factor = 0:
x - 5 = 0
x = 5
Setting the second factor, the trinomial, = 0:
x² + 3x - 2 = 0
We use the quadratic formula:
a = 1, b = 3, c = -2
So the three roots are
5, 
, 
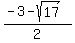Edwin
