Question 409846: what is an indirect proof of Theorem 11.9 (area of a circle)?
*the area of a circle is pi times the square of the radius.
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! The indirect way would be to assume that the area is not equal to  and find a contradiction. However this would involve finding the actual area of a circle, so an indirect proof is unnecessary. and find a contradiction. However this would involve finding the actual area of a circle, so an indirect proof is unnecessary.
Instead, construct a regular n-gon with n isosceles triangles (similar to "Theorem 11.8 which I recently solved, you can find it under the solutions I posted). Instead of finding the length of the base, we find the area, and multiply by n.

Recall that the area of the triangle is 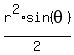 where where  . We have n of these triangles, so the area of the n-gon is . We have n of these triangles, so the area of the n-gon is
 (this may or may not be a good formula to memorize, but it's more important to know where it came from). Take the limit as n goes to infinity: (this may or may not be a good formula to memorize, but it's more important to know where it came from). Take the limit as n goes to infinity:
 . Just like the last problem, if we let . Just like the last problem, if we let  , ,
 . Applying L'Hopital's rule, . Applying L'Hopital's rule,
 . Since . Since  (by direct substitution and noting we obtain a finite and determinate number), (by direct substitution and noting we obtain a finite and determinate number),
 , hence the area of a circle. , hence the area of a circle.
|
|
|