Question 409629: Given 60=2^2 x 3 x 5 and 1050=2 x 3x 5^2 x 7, find
(a) the smallest integer m such that 60m is a perfect cube
(b) the smallest positive integer value of n for which 60n is a multiple of 1050.
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since  we can find the smallest (positive) integer such that the prime factors of 60 all have exponents of multiples of 3. Since the exponents of 2, 3, and 5 are 2, 1, 1 respectively, then m can have 2, 3, 5 exponents of 1, 2, 2 respectively. Therefore we can find the smallest (positive) integer such that the prime factors of 60 all have exponents of multiples of 3. Since the exponents of 2, 3, and 5 are 2, 1, 1 respectively, then m can have 2, 3, 5 exponents of 1, 2, 2 respectively. Therefore  . .
We want 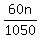 to be an integer. The fraction reduces to to be an integer. The fraction reduces to 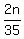 , hence n = 35 is the smallest integer value, as 2 and 35 are relatively prime. , hence n = 35 is the smallest integer value, as 2 and 35 are relatively prime.
|
|
|