SOLUTION: How do I simplify the perfect fourth power factors? 4√16*4√x^12*4√y^12*4√4y^2 Thank you!

Algebra ->  Radicals -> SOLUTION: How do I simplify the perfect fourth power factors? 4√16*4√x^12*4√y^12*4√4y^2 Thank you!      Log On


   

Question 408044: How do I simplify the perfect fourth power factors?
4√16*4√x^12*4√y^12*4√4y^2
Thank you!
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Please use language like "4th root of 16", etc. What you wrote looks like "4 times the square root of 16". I was able to figure out that these were 4th roots only because you happened to mention them.

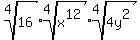
root%284%2C+16%29%2Aroot%284%2C+x%5E12%29%2Aroot%284%2C+4y%5E2%29
Simplifying the 4th roots is easier if you write the radicand (the expression inside a radical is called a radicand) as a power of 4:
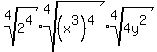
root%284%2C+2%5E4%29%2Aroot%284%2C+%28x%5E3%29%5E4%29%2Aroot%284%2C+4y%5E2%29
Now the first two roots simplify:
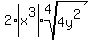
2%2Aabs%28x%5E3%29%2Aroot%284%2C+4y%5E2%29
or
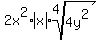
2x%5E2%2Aabs%28x%29%2Aroot%284%2C+4y%5E2%29

The tricky part is the absolute value. All even-numbered roots (square roots , 4th roots, etc.) are non-negative (positive or zero). So when you simplify 4th roots, the simplified expression must be just as non-negative as the original expression. This is why absolute values are sometimes needed.

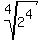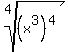When simplifying root%284%2C+2%5E4%29 we don't need absolute value on the 2 because it is positive. But when we simplify root%284%2C+%28x%5E3%29%5E4%29 we need absolute value. This is so because we do not know what x might be and if x was negative x%5E3 would be negative, too.

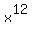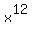Sometimes the original expression will "tell" what values the variable(s) can have. Radicands of even-numbered roots must be non-negative, too. But the original expression, with the x%5E12 in the radicand, allows x to be anything because no matter what x is, x%5E12 will be non-negative. On the other hand, if the original expression had been:
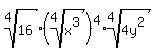
root%284%2C+16%29%2A%28root%284%2C+x%5E3%29%29%5E4%2Aroot%284%2C+4y%5E2%29
it would still simplify to
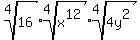
root%284%2C+16%29%2Aroot%284%2C+x%5E12%29%2Aroot%284%2C+4y%5E2%29
However the x%5E3, as a radicand of an even-numbered root in the original expression, must be non-negative. And for x%5E3 to be non-negative, x must be non-negative. So
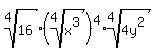
root%284%2C+16%29%2A%28root%284%2C+x%5E3%29%29%5E4%2Aroot%284%2C+4y%5E2%29
would simplify to:
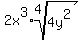
2x%5E3%2Aroot%284%2C+4y%5E2%29
without the absolute value because we already know that x%5E3 is non-negative.

Note 1: Many times problems like these include a statement something like "all variables are non-negative." If so, then absolute values are not needed. So if such a statement was part of your problem, then the answer would just be:
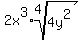
2x%5E3%2Aroot%284%2C+4y%5E2%29

Note 2: Even-numbered roots are non-negative and they must have non-negative radicands. Odd-numbered roots (cube roots, 5th roots, etc.) and their radicands can be anything. So absolute values are never used with odd-numbered roots.

P.S. In response to the comment in your "thank you"...
If you want to see how I made the 4th roots look like they did in my solution, just click on "Show source" above. It will show you what I typed. Look for 3 left braces. "{", and 3 right braces, "}". Between them you will find the text that causes Algebra.com's software to draw the radicals, For example, root(4, 16) (between the braces) causes the 4th root of 16 to be drawn. If you typed root(3, 16) between the braces you would get the cube root of 16 drawn. By changing the first number after the parentheses you can get any kind of root drawn.

P.P.S. For square roots there is a short cut. sqrt(7) (between the braces) causes the square root of 7 to be drawn. (If you type root(2, 7) between the braces you will also get a square root of 7 (with the index of 2 showing).