SOLUTION: find consecutive 2 digit numbers that add to 600

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: find consecutive 2 digit numbers that add to 600       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 407902: find consecutive 2 digit numbers that add to 600
Found 2 solutions by graphmatics, richard1234:
Answer by graphmatics(170) About Me  (Show Source):
You can put this solution on YOUR website!
Let x be the first 2 digit number. Then x+1 is the next consecutive 2
digit number. The problem mentioned looks for the solution of
x+(x+1)=600 but the solution x is not an integer so there is no
solution to the problem.
If we consider the problem using the problem the product of the two
digit numbers is 600 we get two correct answers. We have that
x*(x+1) = 600
x^2 + x + -600 = 0

Solved by pluggable solver: EXPLAIN simplification of an expression
Your Result:


YOUR ANSWER


  • This is an equation! Solutions: x=24,x=-25.
  • Graphical form: Equation x%2A%28x%2B1%29=600 was fully solved.
  • Text form: x*(x+1)=600 simplifies to 0=0
  • Cartoon (animation) form: simplify_cartoon%28+x%2A%28x%2B1%29=600+%29
    For tutors: simplify_cartoon( x*(x+1)=600 )
  • If you have a website, here's a link to this solution.

DETAILED EXPLANATION

Look at x%2A%28x%2B1%29=highlight_red%28+600+%29.
Moved these terms to the left highlight_green%28+-600+%29
It becomes x%2A%28x%2B1%29-highlight_green%28+600+%29=0.
Look at highlight_red%28+x%2A%28x%2B1%29+%29-600=0.
Expanded term x by using associative property on %28x%2B1%29
It becomes highlight_green%28+x%2Ax+%29%2Bhighlight_green%28+x%2A1+%29-600=0.
Look at x%2Ax%2Bx%2Ahighlight_red%28+1+%29-600=0.
Remove extraneous '1' from product highlight_red%28+1+%29
It becomes x%2Ax%2Bx-600=0.
Look at highlight_red%28+x+%29%2Ahighlight_red%28+x+%29%2Bx-600=0.
Reduce similar several occurrences of highlight_red%28+x+%29 to highlight_green%28+x%5E2+%29
It becomes highlight_green%28+x%5E2+%29%2Bx-600=0.
Look at highlight_red%28+x%5E2%2Bx-600+%29=0.
Equation highlight_red%28+x%5E2%2Bx-600=0+%29 is a quadratic equation: x^2+x-600 =0, and has solutions 24,-25
It becomes highlight_green%28+0+%29=0.
Result: 0=0
This is an equation! Solutions: x=24,x=-25.

Universal Simplifier and Solver


Done!

+graph%28+300%2C+200%2C+-40%2C+40%2C+-1000%2C+1000%2C+0%2C+x%5E2%2Bx-600%29+


If x = 24 then 24*25 = 600. If x = -25 then -25*-24 = 600.

Answer by richard1234(7193) About Me  (Show Source):
You can put this solution on YOUR website!
We want the sum of n consecutive two-digit numbers to be 600. Suppose that x, x+1, x+2, ..., x+n-1 are the two digit numbers, and

sum%28x%2Bi%2C+i=0%2C+n-1%29+=+600

This implies that xn+%2B+sum%28i%2C+i=1%2C+n-1%29+=+600 --> xn+%2B+%28n-1%29%28n%29%2F2+=+600, where x > 10 and x+n-1 < 100.

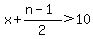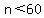Factoring our equation, this becomes n%28x+%2B+%28%28n-1%29%2F2%29%29+=+600. Since x+%2B+%28n-1%29%2F2+%3E+10, it follows that n+%3C+60. We can plug in odd numbers n (so that (n-1)/2 remains an integer) that are factors of 600 (note that 600 = 8*75, so we list all factors of 75):

n:------- x:
1 ------- 600
3 ------- 199
5 ------- 118
15------- 33
25------- 12
75------- -29

The only cases that satisfy are {33, 34, 35, ..., 47} and {12, 14, 15, ..., 36}. It can be checked that their sums are 600.