|
Question 407387: Solve the quadratic system.
Solve algebraically: 4x^2-9y^2=108 and xy=-12
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! xy=-12
y=-12/x
4x^2-9y^2=108
4x^2-9(-12/x)^2=108
4x^2-9(144/x^2)=108
4x^4-1296=108x^2
4x^4-108x^2-1296=0
4z^2-108z-1296=0
Notice we have a quadratic equation in the form of 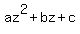 where where  , ,  , and , and 
Let's use the quadratic formula to solve for z
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Negate Negate 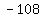 to get to get  . .
 Square Square 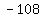 to get to get  . .
 Multiply Multiply 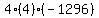 to get to get 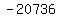
 Rewrite Rewrite 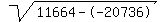 as as 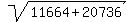
 Add Add  to to  to get to get 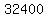
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of 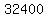 to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the answers in terms of z are  or or 
Now above, I let z = x^2. So x^2 = 36 and x^2 = -9
Solve for x in each equation to get: x = 6, x = -6, x = 3i, or x = -3i
So the four solutions for x are x = 6, x = -6, x = 3i, or x = -3i
Now plug all of these x values into y = -12/x to find the corresponding values of y. I'll let you do this.
In the end, you should have 4 ordered pairs.
If you need more help, email me at jim_thompson5910@hotmail.com
Also, please consider visiting my website: http://www.freewebs.com/jimthompson5910/home.html and making a donation. Thank you
Jim
|
|
|
| |