Question 406950: Im studying right now in College Algebra... parallel and perpendicular lines
I'm stuck on one of those questions. The instructions says to find the equation of the line satisfying the given conditions, giving it in slope-intercept form if possible.
Through (1,6) perpendicular to 3x+5y=1
I know that this is the answer, because a friend tried explaining it to me but I still don't understand how she got this answer.
y=5/3x+13/3
can you please help me
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Im studying right now in College Algebra... parallel and perpendicular lines
I'm stuck on one of those questions. The instructions says to find the equation of the line satisfying the given conditions, giving it in slope-intercept form if possible.
Through (1,6) perpendicular to 3x+5y=1
I know that this is the answer, because a friend tried explaining it to me but I still don't understand how she got this answer.
y=5/3x+13/3
..
The standard slope-intercept form is: y=mx+b, m=slope, and b=y-intercept.
So, to solve your problem, you must find the slope,m, and y-intercept,b.
..
First rule to know is that the slope of a line perpendicular to another line is equal to the negative reciprocal of that line. The problem states that the slope you are trying to find is perpendicular to the slope of the line from the equation, 3x+5y=1. So, all we have to do is find the slope of this line and take its negative reciprocal and apply it to the new equation. To do this, change this equation to a standard form:
3x+5y=1
5y=-3x+1
y=-(3/5)x+1
This says the slope of this line is -(3/5). Its negative reciprcal would then be 5/3. Now, we need to find b, the y-intercept. We will use the given (x,y) coordinates (1/6). With your equation partially solved,
y=5/3x+b
replace x & y with 1 & 6, and solve for b
6=(5/3)(1)+b
b=6-(5/3)
b=(18/3)-(5/3)=13/3
so your new equation is: y=(5/3)x+13/3 (as your friend explained to you)
There is an alternate method using the point-slope formula, but that is for another lesson.
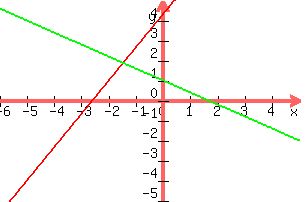
Below is a graph of the two lines involved in the solution. Note how the lines are perpendicular to each other and their y-intercepts.
..
|
|
|