Question 406416: oh boy do i ever need help i am so lost!!!!
1)i need to select any two integers between -12 and +12 which will become solutions to a system of two equations.
2)then i have to write two equations that have my two integers as solutions. I have to show how i built the equationsusing my integers.
3)then i have to solve my system of equations by the addition/ subtration method showing the necessary 5 steps.
Please somebody help me with this my brain feels fried!
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1)i need to select any two integers between -12 and +12 which will become
solutions to a system of two equations.
:
Let's choose the two integers: x=4, y=-6
:
2)then i have to write two equations that have my two integers as solutions. I have to show how i built the equations using my integers.
:
Choose a different slope for each equation, keeping the x, y values of 4,-6
Slope of equation one m=3, use the point/slope formula y - y1 = m(x - x1)
y - (-6) = 3(x - 4)
y + 6 = 3x - 12
y = 3x - 12 - 6
y = 3x - 18
Put equation into the standard form
-3x + y = -18; that's our 1st equation
:
m = -3, using the same x,y values of 4,-6
y - (-6) = -3(x - 4)
y + 6 = -3x + 12
y = -3x + 12 - 6
y = -3x + 6
Put equation into the standard form
3x + y = 6; that's our 2nd equation
;
:
3)then i have to solve my system of equations by the addition/ subtraction method showing the necessary 5 steps.
:
our two equations
-3x + y = -18
+3x + y = 6
-------------------addition eliminates x, find y
0 + 2y = -12
y = 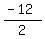
y = -6, which is our chosen value for y
and
3x + y = 6, replace y with -6
3x - 6 = 6
3x = 6 + 6
3x = 12
x = 
x = 4, which is our chosen value for x, right?
:
:
I am not sure about the 5 steps, but did you see how we constructed both
equation using the same x,y value, therefore these value has to be the
solution to the two equations, right? Did I make this understandable to you?
|
|
|