Question 40614: Tell whether the points are the vertices of a parallelogram (that is not a rectangle), a rectangle, or neither.
(-7, -1), (2, -10), (16, -3), (7, 8)
Answer by smik(40)   (Show Source): (Show Source):
You can put this solution on YOUR website! Good Question. For this problem it's good to have some visual aid (a graph) with you. First off you can graph all the points, or just imagine them on a graph in your head. From this, we can tell which point is connected to which if it is to even qualify as a parallelogram. So here's a summary of the links:
Line 1: (-7,-1) to (2,-10)
Line 2: (2,-10) to (16, -3)
Line 3: (16,-3) to (7,8)
Line 4: (7,8) to (-7,-1)
Now, if this is a parallelogram, Line 1 and 3 will be parallel and Line 2 and 4 will be parallel. In other words, they'll have the same slope. Furthermore, if its a rectangle then the slope of Line 1 and 3 will be the negative reciprocal of the slope of Line 2 and 4. Slope is measured by: 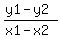
Slope of Line 1: 
Slope of Line 2: 
Slope of Line 3: 
Slope of Line 4: 
From the above, we can come to the conclusion that the graph is neither a rectangle nor a parallelogram.
|
|
|