Question 404518: (9/5)log4x = -2
is the 9/5 the exponent on the logx base 4?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
The first thing to do in solving this equation is to move the 9/5. There are two ways to do this:- We could just multiply both sides by 5/9 giving us:
 - Or use a property of logarithms,
 , which allows you to move a coefficient like 9/5 into the argument as its exponent. Using this property on your equation we get:
This may have been what you were thinking when you asked. "is the 9/5 the exponent on the logx base 4?"
Both of these will work and they will give you the same answer. I will do both. The first one looks easier so we will start with that approach. Now that the equation is in the form:
log(expression) = other-expression
we can proceed to the next step which is to rewrite the equation in exponential form. In general  is equivalent to  . Using this pattern on our equation we get:
This may be an acceptable answer. But we can simplify the right side. If you have trouble with negative or fractional exponents I find it can be helpful to factor the exponent in a certain way:- If the exponent is negative, then factor out -1.
- If the exponent is fractional and the numerator is not a 1, then factor out the numerator. (You'll see what this means shortly,)
Once the exponent is factored, each factor tells you an operation to be done. And, since multiplication is Commutative, these operations can be done in any order! So it is to your advantage to choose the order which makes it the easiest.
Let's see this in action.
1) The exponent is negative so we'll factor out -1:
2) The exponent is fractional and the numerator is 10. So we will factor out 10:
Now let's examine the factored exponent:- The -1 as an exponent means we will be finding a reciprocal.
- The 10 as an exponent means we will be raising to the 10th power.
- The 1/9 as an exponent tells us that we will be finding a 9th root.
A reciprocal will create a fraction. Raising to the 10th power will make the number large and the 9th root doesn't look easy either. So there is not an obviously easier order to use. I will do 10th power, 9th root and then reciprocal:
For reasons we will see shortly, I am going to leave 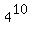 alone for a minute. Changing the exponent of 1/9 to radical form we get:
We can simplify the radical by factoring out power of 9 factors:
(Do you see now why I didn't bother raising 4 to the 10th power?)
Last of all, the reciprocal:
This may also be an acceptable answer. But it does have an irrational denominator. Rationalizing the denominator goes something like this:
This is our solution. (With equations like this, you must check to see that your solution(s) make the arguments of all logarithms positive. Since the solution for x is positive and since the argument of the only logarithm in the original equation is just x, we can quickly see that this answer will make the argument positive. (If our "solution" had made the argument zero or negative we would have to reject that solution.))
If we had made the other first step our equation would be:
Just like before, the next step is to rewrite the equation in exponential form:
To solve for x, we need to find a way to change the exponent from 9/5 to a 1. To do so we will combine three ideas:- It is OK to raise both sides of an equation by the same power.
- The rule for exponents when raising a power to a power is to multiply the exponents.
- Multiplying reciprocals always results in a 1!
Putting these idea together we can turn the exponent of 9/5 into a 1 by raising both sides of the equation by the reciprocal of 9/5 power! The reciprocal of 9/5 is 5/9:
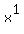On the left side we get  (or "x") just as we planned. On the right side we get:
This is the same equation as we got with the other first step and its solution from this point on is the same as above.
|
|
|
