SOLUTION: The square root of x raised to the 3rd power divided by the square root of 12

Algebra ->  Square-cubic-other-roots -> SOLUTION: The square root of x raised to the 3rd power divided by the square root of 12      Log On


   

Question 404197: The square root of x raised to the 3rd power divided by the square root of 12
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!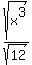
sqrt%28x%5E3%29%2Fsqrt%2812%29
While there are other ways, the way I like to simplify radical over radical fractions is:
  1. Use a property of radicals, root%28a%2C+p%29%2Froot%28a%2C+q%29+=+root%28a%2C+p%2Fq%29, to rewrite the fraction of radicals into the radical of a fraction.
  2. Reduce the fraction inside the radical, if possible.
  3. Multiply the numerator and denominator of the fraction by the same expression so that the denominator a power of the type of root. (Since you have square roots we will be making the denominator a perfect square. If they had been cube roots, we would make the denominator a perfect cube. If they had been 4th roots, etc.)
  4. Use the root%28a%2C+p%29%2Froot%28a%2C+q%29+=+root%28a%2C+p%2Fq%29 property again, this time from right to left, to rewrite the radical of a fraction as a fraction of radicals.
  5. Simplify the two radicals. If step 3 was done correctly then the radical in the denominator should disappear.

Let's see this in action.
1) Use the property to combine the radicals:
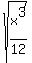
sqrt%28x%5E3%2F12%29
2) Reduce the fraction inside the radical, if possible.
This fraction, x%5E3%2F12, will not reduce.
3) Multiply the numerator and denominator so that the denominator inside the radical becomes a power of the type of root.
In this expression we will make the denominator into a perfect square. The obvious choice would be to multiply the numerator and denominator by 12. But we can do better: Multiplying the numerator and denominator by 3. This will make the denominator a 36 which is a perfect square. The lower perfect square saves us from extra simplifying later on.
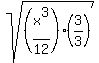
sqrt%28%28x%5E3%2F12%29%283%2F3%29%29
giving us:
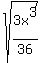
sqrt%283x%5E3%2F36%29
4) Use the property to split the radicals:
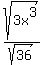
sqrt%283x%5E3%29%2Fsqrt%2836%29
5) Simplify the radicals.
The denominator, being the square root of a perfect square, simplifies to a nice whole number. The numerator is not a perfect square. But it does have a perfect square factor:
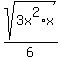
sqrt%283x%5E2%2Ax%29%2F6
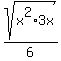
sqrt%28x%5E2%2A3x%29%2F6
%28sqrt%28x%5E2%29%2Asqrt%283x%29%29%2F6
%28x%2Asqrt%283x%29%29%2F6
This is the simplified answer.

When we were making the denominator a perfect square we turned it into a 36. If we had used the more obvious choice, here is how it would have worked out:
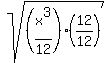
sqrt%28%28x%5E3%2F12%29%2812%2F12%29%29
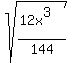
sqrt%28%2812x%5E3%29%2F144%29
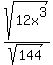
sqrt%2812x%5E3%29%2Fsqrt%28144%29
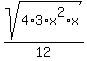
sqrt%284%2A3%2Ax%5E2%2Ax%29%2F12
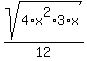
sqrt%284%2Ax%5E2%2A3%2Ax%29%2F12
%28sqrt%284%29%2Asqrt%28x%5E2%29%2Asqrt%283%2Ax%29%29%2F12
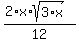
%282%2Ax%2Asqrt%283%2Ax%29%29%2F12
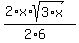
%282%2Ax%2Asqrt%283%2Ax%29%29%2F%282%2A6%29
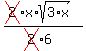
%28cross%282%29%2Ax%2Asqrt%283%2Ax%29%29%2F%28cross%282%29%2A6%29
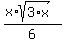
%28x%2Asqrt%283%2Ax%29%29%2F6
We get the same answer. But did you notice the extra simplifying?