Question 404050: consider the following infinite sequence of numbers 17, 24, 31, 38, 45, 52. what is the least term in the sequence that is a multiple of 2, 3, 4, 5, 6?
Found 2 solutions by Edwin McCravy, richard1234:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
17, 24, 31, 38, 45, 52
That is an arithmetic sequence with a1 = 17 and d = 7
The nth term of an arithmetic sequence is given by
an = a1 + (n - 1)d
an = 17 + (n - 1)(7)
an = 17 + 7n - 7
an = 10 + 7n
To be a multiple of 2, 3, 4, 5, 6, is to be a multiple of 2*2*3*5 = 60
So we are looking for the smallest integer k so that
10 + 7n = 60k
Write the 10 and the 60 in terms of their nearest multiples of 7.
10 is nearest 7 and 60 is nearest 63
(7 + 3) + 7n = (63 - 3)k
7 + 3 + 7n = 63k - 3k
Divide through by 7
1 + 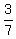 + n = 9k - + n = 9k - 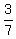 k
Isolate the fractional terms: k
Isolate the fractional terms:
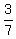 + + 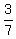 k = 9k - n - 1
Since the right side is an integer, the left side is also an integer.
Let that integer be A. k = 9k - n - 1
Since the right side is an integer, the left side is also an integer.
Let that integer be A.
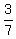 + + 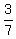 k = A and 9k - n - 1 = A
Clear of fractions:
3 + 3k = 7A
Write the 7 in terms of its nearest multiple of 3, which is 6
3 + 3k = (6 + 1)A
3 + 3k = 6A + A
Divide through by 3
1 + k = 2A + k = A and 9k - n - 1 = A
Clear of fractions:
3 + 3k = 7A
Write the 7 in terms of its nearest multiple of 3, which is 6
3 + 3k = (6 + 1)A
3 + 3k = 6A + A
Divide through by 3
1 + k = 2A + 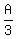 Isolate the fraction:
1 + k - 2A =
Isolate the fraction:
1 + k - 2A = 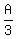 Since the left side is an integer, the right side is also an integer.
Let that integer be B.
Since the left side is an integer, the right side is also an integer.
Let that integer be B.
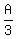 = B and 1 + k - 2A = B
Clear of fractions:
A = 3B
Substituting in 1 + k - 2A = B
1 + k - 2(3B) = B
1 + k = 6B + B
1 + k = 7B
k = 7B - 1
Substituting for A and k in 9k - n - 1 = A
9(7B - 1) - n - 1 = 3B
63B - 9 - n - 1 = 3B
63B - 10 - n = 3B
60B - 10 = n
The smallest possible value of B that would produce
a positive value for n is 1, thus B = 1
60(1) - 10 = n
50 = n
and k = 7B - 1 = 7(1) - 1 = 6
Therefore the desired term is the 50th. That term can be
gotten from either
10 + 7n = 10 + 7(50) = 10 + 350 = 360
or from
60k = 60(6) = 360.
So the answer is 360, which is the 50th term.
Edwin = B and 1 + k - 2A = B
Clear of fractions:
A = 3B
Substituting in 1 + k - 2A = B
1 + k - 2(3B) = B
1 + k = 6B + B
1 + k = 7B
k = 7B - 1
Substituting for A and k in 9k - n - 1 = A
9(7B - 1) - n - 1 = 3B
63B - 9 - n - 1 = 3B
63B - 10 - n = 3B
60B - 10 = n
The smallest possible value of B that would produce
a positive value for n is 1, thus B = 1
60(1) - 10 = n
50 = n
and k = 7B - 1 = 7(1) - 1 = 6
Therefore the desired term is the 50th. That term can be
gotten from either
10 + 7n = 10 + 7(50) = 10 + 350 = 360
or from
60k = 60(6) = 360.
So the answer is 360, which is the 50th term.
Edwin
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! We want the least term that is a multiple of the LCM of 2, 3, ..., 6, or 60.
Our sequence is denoted by 17 + 7k, where k is an integer. Writing everything modulo 2, 3, and 5, we obtain
1 + k ≡ 0 (mod 2) --> k ≡ 1 (mod 2)
2 + k ≡ 0 (mod 3) --> k ≡ 1 (mod 3)
2 + 2k ≡ 0 (mod 5) --> 1 + k ≡ 0 (mod 5) --> k ≡ 4 (mod 5)
The first two equations imply k ≡ 1 (mod 6), so k can be 1, 7, 13, 19, 25, 31, ... The first value of k that is 4 modulo 5 is 19, so the smallest term in the sequence that satisfies is 17 + 7(19), or 150.
|
|
|