Question 403836: e^2x-6e^x+8=0
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
The key to a solution to thsi equation is to notice that the expo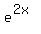nent of the  term is twice the exponent of the 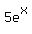 term. This makes the equation in "quadratic form" for  . So we can use methods appropriate for quadratic equations to solve it.
It can be difficult at first to see how to solve these quadratic form equations. A temporary variable can be helpful.
Let  .
Then 
Substituting these into the equation we get:
It should be obvious that this is a quadratic equation. One side is already zero so we can proceed with factoring (or using the Quadratic Formula). This factors fairly easily:
(q-4)(q-2) = 0
From the Zero Product Property we know that this (or any) product can be zero only if one (or more) of the factors is zero. So:
q-4 = 0 or q-2 = 0
Solvign these we get:
q = 4 or q = 2
We have solved for q. But we want to solve to x. Now we replace q with :
 or 
To solve these equations for x, we need to use logarithms. Since the exponential terms have a base of e, it makes sense to use the base e logarithm, ln:
 or 
On the left side of each equation we use a property of logarithms,  , to move the exponent of the argument out in front. (It is this very property that is the reason we use logarithms on equations like these. It allows us to move the exponent, where the variable is, out in front where we can now solve for it.) Using thsi property on both equations we get:
 or 
And by definition, ln(e) = 1. So these equations become:
x = ln(4) or x = ln(2)
These are exact expressions for the two solutions to your equation. If you want decimal approximations, get out your calculator and find the two logarithms. (If your calculator does not have a button for ln, then use the base conversion formula for logarithms to convert these to base 10 logarithms.)
Once you have solved a few of these quadratic form equations you will no longer need the temporary variables. You will learn to see how to go from:
to
to
 or 
etc.
|
|
|
