SOLUTION: Divide ^3 over the square root of 48a^7b^8 over ^3 over the square root of 6a^5b^7 then simplify by taking roots if possible and assume that all expressions under radicals represen

Algebra ->  Square-cubic-other-roots -> SOLUTION: Divide ^3 over the square root of 48a^7b^8 over ^3 over the square root of 6a^5b^7 then simplify by taking roots if possible and assume that all expressions under radicals represen      Log On


   

Question 401444: Divide ^3 over the square root of 48a^7b^8 over ^3 over the square root of 6a^5b^7 then simplify by taking roots if possible and assume that all expressions under radicals represent positive numbers.
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!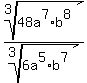
root%283%2C+48a%5E7%2Ab%5E8%29%2Froot%283%2C+6a%5E5%2Ab%5E7%29
First, these are called cube roots. The phrase "square root" has nothing to do with these.

What you are calling a square root is actually the radical symbol. The radical symbol is used for all types of roots. The little number in the upper left corner of the radical is called the index. The index indicates which type of root the radical represents. The index of 3 on your radicals tells us that they represent cube (or 3rd) roots. A radical without a visible index has an implied index of 2 and represents a square (or 2nd) root. This is why radicals and square roots can be easily confused.

There are a variety of ways to divide two radicals. The procedure I prefer is:
  1. Use the property of radicals, root%28a%2C+p%29%2Froot%28a%2C+q%29+=+root%28a%2C+p%2Fq%29, to change the fraction of radicals into a single radical of a fraction.
  2. Reduce the fraction inside the radical.
  3. If there is still a fraction,...
    1. Make the denominator a perfect power of the type of radical. (for square roots make it a perfect square, for cube roots, make it a perfect cube, etc.)
    2. Use the same property as in step #1, except in the reverse direction, to split the radical into a fraction of radicals.
      3. <
    3. Simplify the radical in the numerator, if possible.
    4. Simplify the radical in the denominator. This radical should simplify to an integer.
    5. If all the previous have been done correctly then you should be done. If not, there may be common factors, outside the radical in the numerator to cancel.
    If there is no longer a fraction and there is still a radical, then try to simplify it.

Let's see this in action.
1) Use the property to combine the radicals:
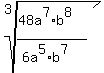
root%283%2C+%2848a%5E7%2Ab%5E8%29%2F%286a%5E5%2Ab%5E7%29%29
2) Reduce the fraction.
root%283%2C+%286%2A8%2Aa%5E5%2Aa%5E2%2Ab%5E7%2Ab%29%2F%286a%5E5%2Ab%5E7%29%29

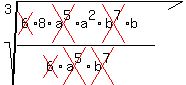
leaving
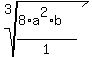
root%283%2C+%288%2Aa%5E2%2Ab%29%2F1%29
which simplifies to
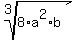
root%283%2C+8%2Aa%5E2%2Ab%29
3) There is no fraction left but there is a radical. So we try to simplify it. Simplifying a cube root involves finding perfect cube factors. 8 is a perfect cube, 2%5E3. But there are no perfect cube factors in a%5E2 or b. Since we did find a perfect cube factor, 8, we can simplify. We use another property of radicals, root%28a%2C+p%29%2Aroot%28a%2C+q%29+=+root%28a%2C+p%2Aq%29, (from right to left) to split up the one cube root. We want the perfect cube(s) each in their own cube root and all the other factors into another cube root:
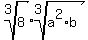
root%283%2C+8%29%2Aroot%283%2C+a%5E2%2Ab%29
The cube root of 8 is 2 so this becomes:
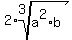
2%2Aroot%283%2C+a%5E2%2Ab%29
And we are finished.

P.S. The part about "all expressions under radicals represent positive numbers" is irrelevant for an odd-numbered root like a cube root.