Question 400822: what is the domain of √ ̅ (x-3) divided by x^2-8x+12?
Found 2 solutions by nerdybill, robertb:
Answer by nerdybill(7384)   (Show Source):
You can put this solution on YOUR website! "Domain" specifies the "range of values" x can take for the given function.
.
In your case, there are two conditions
- you don't want the stuff under the radical to be negative, because the square root of a negative produces an imaginary number
x-3 >= 0
x >= 3
that is, 'x' is greater than or equal to 3
.
- And, you don't want a zero in the denominator (because that produces an "undefined" number)
to find what value x can't take we set
x^2-8x+12
to zero and solve for x:
x^2-8x+12 = 0
(x+2)(x-6) = 0
x = {-2, 6}
.
Solution:
Domain x >= 3 AND "x does not = 6"
Or,
[3,6) U (6, +oo)
where
oo represents infinity
Answer by robertb(5830)  (Show Source):
You can put this solution on YOUR website! If your rational function is  , then the domain is obtained as follows:
From the expression  , the critical numbers are 2, 3, and 6. These critical numbers partition the real number line into the intervals ( , 2), (2, 3), (3, 6), (6,  ).
At (, 2), 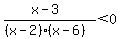 by using the test point x = 0.
At (2, 3), 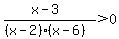 by using the test point x = 2.5.
At (3, 6), 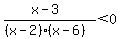by using the test point x = 4.
At (6, ), 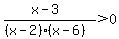by using the test point x = 7.
The critical numbers 2 and 6 are not included in the domain, as these will make the denominator equal to 0. We want those intervals that will make 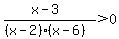, because the whole expression is under the square root symbol. The critical number x = 3 is included in the domain.
Hence the domain of the rational function is (2,3]U(6, ).
|
|
|
