Question 400630: let{u1,u2....uk}be a linearly independent set of vector in R^n and c1,c2,....ck are scalars. prove that {c1u1, c2u2....., ckuk}is also limearly independent.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since {  , , , , 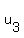 , ..., , ...,  } are linearly independent, then the equation } are linearly independent, then the equation  + ...+ + ...+  has only the trivial solution has only the trivial solution  = ...= = ...=  . ( . (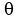 is the zero vector, and is the zero vector, and 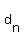 's are scalars.) 's are scalars.)
We have to assume that none of the 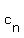 's are equal to zero, otherwise, 's are equal to zero, otherwise,
{  , , , ,  , ..., , ...,  } would contain the zero vector, automatically making the set linearly dependent. Hence } would contain the zero vector, automatically making the set linearly dependent. Hence
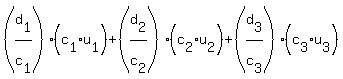 + ...+ + ...+ 
==>  for every n = 1,2,3,...,k, and { for every n = 1,2,3,...,k, and {  , , , ,  , ..., , ...,  } is a linearly independent set. } is a linearly independent set.
|
|
|