Question 400450: How to solve
x4-5x3+7x2-5x+6;-i
Please help
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please post the entire problem. There is no way this is exactly how it was given to you. And use "^" to indicate exponents. For example:
x^4-5x^3+7x^2-5x+6
I'm guessing the problem is something like: "Find the remaining roots (or zeros) of 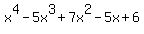 given that one of them is -i." given that one of them is -i."
Roots (or zeros) of a polynomial are values for the variable that make the polynomial equal to zero. And if "r" is a root of a polynomial then (x-r) is a factor of the polynomial.
The fact that -i is a root of the polynomial tells you three things:- (x-(-i)), or (x+i), is a factor of the polynomial.
- If there are complex roots, like -i, of a polynomials with real coefficients, like yours, then the complex roots come in conjugate pairs. In general a+bi and a-bi (or a+(-bi)) are a conjugate pair. So if -i, or 0 + (-i), is a root, then its conjugate, 0 + i (or just i) is also a root.
- If i is a root, then (x-i) is a factor.
So we have two roots, i and -i, so far. Your polynomial is a 4th degree polynomial (because the highest exponent is 4) and so it should have 4 roots. To find other two roots we will factor it.
Since (x+i) and (x-i) are factors they will divide into the polynomial evenly. And the quotient will be the other factor. So we will divide by the known factors (using synthetic division):
-i | 1 -5 7 -5 6
---- -i -1+5i 5-6i -6
----------------------------
1 -5-i 6+5i -6i 0
So  . Now we will divide the second factor by the other known factor, (x-i): . Now we will divide the second factor by the other known factor, (x-i):
i | 1 -5-i 6+5i -6i
---- i -5i 6i
---------------------------
1 -5 6 0
So now we have:

To find the last two roots we will factor the third factor. This is a fairly simple trinomial to factor:

Remembering that if "r" is a root then (x-r) is a factor (and vice versa), we can see that the 4 roots of 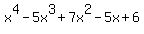 are: -i, i, 2 and 3. are: -i, i, 2 and 3.
|
|
|