Question 398616: x^-3/2=1/729
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
The solution to this problem will be of the form
x = something
And since x and 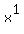 are the same thing, one way to look at the task ahead is: How do we change an exponent of -3/2 into a 1? To accomplish this we will put together 3 ideas: are the same thing, one way to look at the task ahead is: How do we change an exponent of -3/2 into a 1? To accomplish this we will put together 3 ideas:- It is OK to raise both sides of an equation to the same power.
- The rule for exponents when raising a power to a power is to multiply the exponents.
- Multiplying reciprocals always results in 1!
So by raising both sides of this equation to the reciprocal of -3/2 power, the exponent will turn into a 1. The reciprocal of -3/2 is -2/3:

On the left we end up with x, as planned:

Now we just need to simplify the right side. If you have trouble with negative and/or fractional exponents,I find that it can be helpful to factor the exponent in a certain way:- If the exponent is negative, factor out a -1.
- If the exponent is fractional and its numerator is not a 1, factor out the numerator.
Factoring the exponent of -2/3 in this way we first factor out -1:

The fraction in the exponent does not have a numerator of 1 so we factor out the 2:

Looking at the factors in the exponent we can see that there will be three operations to perform:- The -1 (as an exponent) tells us that we will find a reciprocal.
- The 2 (as an exponent) tells us that we willbe squaring.
- The 1/3 (as an exponent) tells us (if you remember what fractional exponents mean) that we will be finding a cube root.
And since multiplication is Commutative, we can do these three operations in any order we choose! So let's choose the order that looks easiest. Finding a reciprocal of a fraction is pretty simple (just flip it upside down). And since the 1 in the fraction will end up in the denominator the reciprocal of 1/729 ends up being the nice whole number 729! So it looks like starting with the reciprocal is the easiest first step. Next we will square or find a cube root. Since squaring 729 and then finding a cube root does not look appealing, I am going to find a cube root and then square. Rearranging the factors in the chosen order we get:

which is equal to:

Now we can simplify, from the inside out:

or

With a little effort we can find that the cube root of 729 is 9:

which simplifies to:
x = 81
Note: If you choose a different order, the answer works out the same!
|
|
|